- Szerző Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:34.
- Utoljára módosítva 2025-01-23 12:20.
A sebesség annak a kiszámítása, hogy milyen gyorsan mozog valami egyszerre. Ha valaha is nézte a mozgó autó sebességmérőjét, látni fogja a sebességszámot - minél tovább halad a tű, annál nagyobb a jármű sebessége. A sebesség kiszámításának számos módja van, a rendelkezésre álló információk típusától függően. Általában a képlet sebesség = távolság/idő (vagy k = j/w) a legegyszerűbb módja a sebesség kiszámításának.
Lépés
1. módszer a 3 -ból: Standard sebességszámítási képletek használata

1. lépés. Keresse meg az objektum megtett távolságát
Az alapvető képlet, amelyet a legtöbb ember használ valami sebességének megtalálásához, nagyon könnyen használható. Először is tudnia kell, hogy „mennyi távolságot tett meg a mért tárgy”. Más szóval, mennyi a távolság az objektum kezdőpontja és végpontja között?
Ezt a képletet könnyebb megérteni egy példán keresztül. Tegyük fel, hogy "161 kilométeren" autóval utazunk egy játszótérre. Néhány lépésben felhasználhatjuk ezeket az információkat a képlet kiszámításához

2. lépés. Keresse meg az időt, ameddig az objektum megteszi ezt a távolságot
A következő információ, amire szüksége van, az, hogy mennyi idő alatt ér el az objektum egy bizonyos távolságot. Más szóval, mennyi ideig tart, amíg az objektum a kezdőpontról a végpontra mozog?
Ebben a példában tegyük fel, hogy az objektum kb. két óra hogy eljusson a célhoz.

Lépés 3. Osztja el a távolságot az idővel, amellyel megtalálja a tárgy sebességét
Az objektum sebességének megismeréséhez csak erre a két információra van szüksége. Az idő távolsága megegyezik a tárgy sebességével.
Ebben a példában 161 kilométer/2 óra = 80,5 kilométer/óra.

4. lépés. Ne felejtse el a használt egységet
Nagyon fontos, hogy a válaszban a megfelelő mértékegységeket használja (például kilométer per óra stb.) Ezen egységek nélkül az embereknek nagyon nehéz megérteniük válaszának jelentését. Pontokat is elveszíthet, ha rossz egységet használ az iskolai feladatok elvégzésekor.
A sebesség mértékegysége távolság mértékegysége az időegységhez. Például, mivel a távolságot kilométerben és az időt órában mérjük, a használt mértékegységek a következők kilométer/óra (vagy kilométer per óra).
2. módszer a 3 -ból: Nehezebb számítások megoldása

1. lépés Keressen több különböző változót a távolság és az idő problémájának megoldásához
Miután megértette a sebesség alapvető képletét, használhatja a sebességtől eltérő számítások elvégzésére. Például, ha először csak az objektum sebességét és egy másik változót ismer, akkor a fenti képletet átrendezheti, hogy megtalálja az ismeretlen információt.
-
Tegyük fel például, hogy tudjuk, hogy egy vonat négy órán keresztül 20 kilométer per óra sebességgel halad, de nem tudjuk, milyen messzire utazott. Ennek kiderítésére a képletet a következő módon rendezhetjük át:
-
- sebesség = távolság/idő
- sebesség × idő = (távolság/idő) × idő
- sebesség × idő = távolság
- 20 km/óra × 4 óra = távolság = 80 kilométer
-

2. lépés Szükség szerint alakítsa át a használt mértékegységeket
Néha kiszámíthatja a sebességet egy bizonyos egység használatával, de át kell alakítania egy másik egységre. Ebben az esetben egy konverziós tényezőt kell használnia, hogy a helyes egységek szerinti választ kapja. Ehhez egyszerűen írja be az egységek közötti kapcsolatot tört alakban, és szorozza meg. Szorzáskor fordítsa meg a törtet szükség szerint, hogy eltávolítsa a nem kívánt egységeket. Ez a módszer sokkal egyszerűbb, mint amilyennek hangzik!
-
Tegyük fel például, hogy a fenti példaproblémában kilométerek helyett mérföldben kell megadni a választ. Egy mérföld körülbelül 1,6 kilométer. Tehát az átalakítást a következőképpen hajthatjuk végre:
-
- 80 kilométer × 1 mérföld/1,6 kilométer = 50 mérföld
-
- Ne feledje, hogy mivel a kilométerek a tört alján jelennek meg, ez eltávolítja a kilométereket az előző válaszból, így a végeredmény mérföldeket használ.
- Ez a webhely a legtöbb általánosan használt egység konverziós funkcióit kínálja.

Lépés 3. Szükség szerint cserélje ki a "távolság" változót a távolság képlettel
A tárgyak nem mindig egyenes, sima úton haladnak. Ha ez igaz, akkor előfordulhat, hogy nem tud egyszerűen megadni egy számértéket távolság mértékegységeként a szabványos sebesség képletbe. Előfordulhat azonban, hogy a k = j/w képlet j betűjét le kell cserélnie egy olyan képletre, amely hasonlít az objektum által megtett távolságra.
-
Tegyük fel például, hogy egy repülőgép 20 mérföldes távolságban ötször forog a levegőben. A gép fél óra alatt teljesítette a kört. Ebben a példában még meg kell találnunk a repülőgép által megtett teljes távolságot, mielőtt meg tudjuk határozni a sebességét. Ebben a képletben j helyett a képletet használhatjuk a kör körüli távolság (körüli távolság) kiszámítására. Ez a képlet a kerület = 2πr ahol r = a kör sugara. A következőképpen oldhatja meg:
-
- k = (2 × × r)/w
- k = (2 × × 10)/0,5
- k = 62,83/0,5 = 125,66 mérföld/óra
-

4. lépés. Értse meg, hogy k = j/w adja az átlagos sebességet
A sebesség megkereséséhez használt egyszerű és egyszerű képletnek van egy hátránya. A kapott érték technikailag az átlagos sebesség. Ez azt jelenti, hogy a képlet feltételezi, hogy a mért tárgy ugyanazt a sebességet használja, mint ahogy mozog. Amint az alábbiakban látni fogjuk, egy objektum sebességének megtalálása egyetlen pillanatban sokkal nehezebb lesz.
Ennek a különbségnek a szemléltetésére képzelje el, mikor utoljára utazott autóval. Nem valószínű, hogy ugyanolyan sebességgel fog utazni, mint utazik. Általában azonban alacsony sebességgel kezdi útját, és fokozatosan növeli sebességét az út mentén, megáll a piros lámpák, a forgalmi dugók stb. Ha a szokásos sebességformulát használja a sebesség keresésére utazás közben, akkor a sebességváltozások nem észlelhetők. Mindazonáltal választ kap, amely megmutatja az összes sebességkülönbség átlagos sebességét
3. módszer 3 -ból: Azonnali sebesség kiszámítása
Jegyzet:
Ez a rész olyan technikákat használ, amelyek kevésbé ismertek azok számára, akik még soha nem tanultak a számításból. Segítségért olvassa el a számításokkal kapcsolatos cikkeinket.
1. lépés. Értsd meg, hogy a sebesség a gyorsulás mértéke
A magas szintű sebességszámítások meglehetősen zavaróak, mivel a matematikusok és tudósok különböző definíciókat használnak a "sebesség" és a "gyorsulás" leírására. A gyorsulásnak két összetevője van: "sebesség" és "irány". Az arány megegyezik az objektum sebességével. Az irányváltozás a gyorsulás változását okozza, de nem a sebességváltozást.
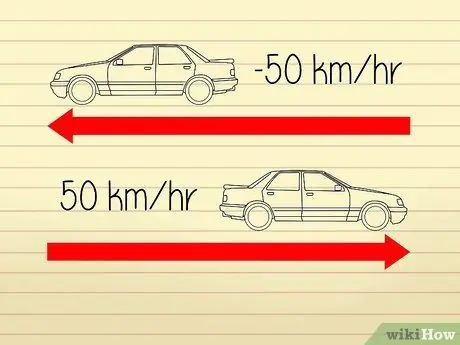
- Tegyük fel például, hogy két autó ellenkező irányba halad. Mindkét autó sebességmérője 50 km/h értéket mutat, így mindketten azonos sebességgel haladnak. Mivel azonban az autók távolodnak egymástól, azt mondhatjuk, hogy az egyik autó gyorsulása -50 km/h, míg a másiké 50 km/h.
- Csakúgy, mint a pillanatnyi sebességszámítások, azonnali gyorsulás számításokat is elvégezheti.

2. lépés Használjon abszolút értékeket a negatív gyorsulás mérésére
Egy objektumnak lehet gyorsulási sebessége (ha negatív irányba mozog egy másik objektumhoz képest). Azonban nincs negatív sebesség. Tehát ebben az esetben a sebesség abszolút értéke jelzi az objektum sebességét.
Emiatt a fenti példaproblémában mindkét autó sebessége 50 km/h.
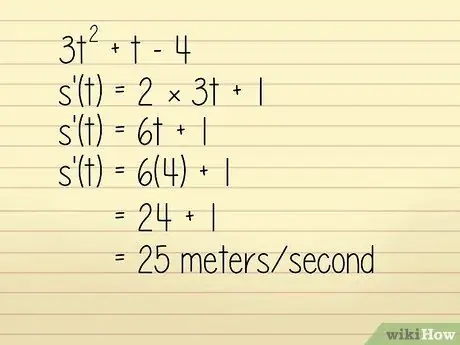
3. lépés Vegyük a függvény pozíciójának deriváltját
Ha van egy k (w) függvénye, amely megmutatja egy objektum helyzetét anélkül, hogy ki kellene számítani az időt, akkor a k (w) deriváltja a gyorsulást mutatja időzítés nélkül. Csak csatlakoztassa az időértéket ebbe a képletbe, hogy a w változó (vagy bármilyen időértéket használjon) az adott idő szerint gyorsuljon. Innen könnyen megtalálhatja az objektum sebességét.
-
Tegyük fel például, hogy egy objektum helyzetét egy méterben a 3q egyenlet írja le2 + w - 4 ahol w = idő másodpercben. Meg akarjuk ismerni az objektum sebességét w = 4 másodpercnél. Ebben az esetben a következőképpen oldhatja meg:
-
- 3w2 +w - 4
- k '(w) = 2 × 3w + 1
- k '(w) = 6w + 1
-
-
Most beírjuk w = 4:
-
- k '(w) = 6 (4) + 1 = 24 + 1 = 25 méter/másodperc. Technikailag ez a gyorsulás számítása, de mivel pozitív, és az irány nem szerepel a kérdésben, használhatjuk a sebesség megtalálására.
-

4. lépés Vegye ki az integrált gyorsítási funkciót
A gyorsítás egy módszer az objektum gyorsulásának időbeli változásának mérésére. Ez a téma túl bonyolult ahhoz, hogy ebben a cikkben teljes mértékben kifejtsük. Hasznos azonban megjegyezni, hogy ha van egy olyan (w) függvénye, amely az idő függvényében gyorsulást jelent, akkor a (w) integrálja visszaadja a gyorsulás eredményét az idő alapján. Ne feledje, nagyon hasznos ismerni az objektum kezdeti gyorsulását, hogy egy végtelen integrálból meghatározhassa az eredmény állandóját.
-
Tegyük fel például, hogy egy objektum állandó gyorsulással rendelkezik (m/s -ban)2 a (w) = -30 eredményeként. Mondja azt is, hogy az objektum kezdeti gyorsulása 10 m/s. Meg kell találnunk a sebességet w = 12 másodpercnél. Ebben az esetben a következőképpen oldhatjuk meg:
-
- a (w) = -30
- p (w) = a (w) dw = -30dw = -30w + C
-
-
A C kereséséhez p (w) -t oldunk meg, ha w = 0. Ne feledje, hogy az objektum kezdeti gyorsulása 10 m/s.
-
- p (0) = 10 = -30 (0) + C
- 10 = C, tehát p (w) = -30w + 10
-
-
Most w = 12 másodpercet írhatunk be.
-
- p (12) = -30 (12) + 10 = -360 + 10 = -350. Mivel a sebesség a gyorsulás abszolút értéke, a tárgy sebessége az 350 méter/másodperc.
-
Tippek
- A gyakorlat nagyszerű! Próbálja meg létrehozni saját kérdését a fenti példaproblémában szereplő számok helyett.
- Ha gyors módszert keres a számítás gyakorlására a jobb számítási sebesség érdekében, használja az online derivált számológépet itt, és az online integrált számológépet itt.






