A Spearman -féle rangkorrelációs együtthatóval azonosíthatjuk, hogy két változónak van -e monoton függvényviszonya (vagyis ha az egyik szám növekszik, akkor a másik is nőni fog, vagy fordítva). A Spearman -féle rangkorrelációs együttható kiszámításához rangsorolni és összehasonlítani kell az adathalmazokat, hogy megtaláljuk a d2, majd írja be az adatokat a szabványos vagy egyszerűsített Spearman -korrelációs együttható képletbe. Ezeket az együtthatókat Excel formulákkal vagy az R paranccsal is kiszámíthatja.
Lépés
Módszer 1 /3: Kézi módszer
1. lépés. Táblázat létrehozása
A táblázat tartalmazza a Spearman -korrelációs együttható kiszámításához szükséges összes információt. Szüksége van egy ilyen táblázatra:
- Hozzon létre 6 oszlopot címsorokkal, mint a példában.
- Készítsen el annyi üres sort, amennyi az adatpárok száma.
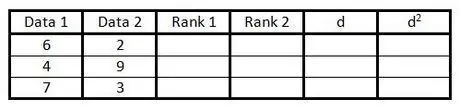
2. Töltse ki az első két oszlopot adatpárokkal
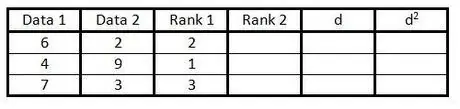
Lépés 3. Írja be az adatcsoportok első oszlopának rangsorolását a harmadik oszlopban 1 -től n -ig (adatok száma)
A legalacsonyabb értékhez adjon 1 -es minősítést, a következő legalacsonyabb értékhez 2 -et stb.
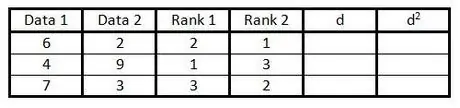
4. lépés. A negyedik oszlopban végezze el ugyanazt, mint a 3. lépésben, de rangsorolja az adatokat a második oszlopban
-
Átlagos_742 Ha két (vagy több) azonos értékű adat van, számítsa ki az adatok átlagos minősítését, majd írja be azokat egy táblázatba ezen átlagérték alapján.
A jobb oldali példában két 5 -ös érték található a 2 -es és a 3 -as értékeléseken. Mivel két 5 -ös van, keresse meg az értékelés átlagát. A 2 és 3 átlaga 2,5, ezért adja meg a 2,5 értéket mindkét érték 5 esetén.
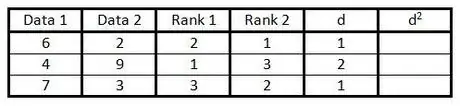
5. lépés. A "d" oszlopban számolja ki a rang oszlopban lévő két szám közötti különbséget
Vagyis ha az egyik oszlop 1, a másik oszlop 3, akkor a különbség 2 (A jel nem számít, mert a következő lépés az érték négyzetbe állítása.)
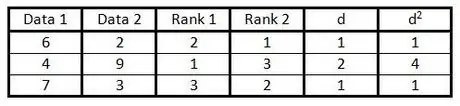
6. lépés Négyzetelje be mindegyik számot a "d" oszlopba, és írja be az eredményt a "d" oszlopba2".
7. lépés. Adja össze az összes adatot a "d" oszlopban2".
Az eredmény d2.
8. lépés. Válasszon az alábbi képletek közül:
-
Ha egyik besorolás sem egyezik meg az előző lépéssel, akkor adja meg ezt az értéket az egyszerűsített Spearman Rank Correlation Coefficient képletben
8_271. Lépés és cserélje ki az "n" -t az adatpárok számával, hogy megkapja az eredményt.
9_402. Lépés -
Ha hasonló rang van az előző lépésben, használja a szabványos Spearman Rank Correlation Coefficient képletet:
Spearman
9. lépés. Értelmezze az eredményeket
Az érték -1 és 1 között változhat.
- Ha az érték közel -1, akkor a korreláció negatív.
- Ha az érték közel 0, akkor nincs lineáris korreláció.
- Ha az érték közel 1, akkor a korreláció pozitív.
2. módszer a 3 -ból: Excel használata
1. lépés Hozzon létre egy új oszlopot az adatokhoz, valamint azok rangsorolását
Például, ha az adatok az A2: A11 oszlopban vannak, használja a "= RANK (A2, A $ 2: A $ 11)" képletet, és másolja le, amíg le nem fedi az összes oszlopot és sort.
2. lépés Változtassa meg ugyanazt a besorolást, amelyet az 1. módszer 3. és 4. lépése ismertet
3. lépés: Az új cellában számítsa ki a korrelációt a két rangoszlop között a "= CORREL (C2: C11, D2: D11)" képlettel
Ebben a példában a C és D arra az oszlopra utal, ahol a rangsor található. Az új cellát a Spearman Rank Correlation fogja kitölteni.
3. módszer 3 -ból: R
1. lépés: Először telepítse az R programot, ha még nem rendelkezik vele
(Lásd:
Lépés 2. Mentse az adatokat CSV formátumban, az első két oszlopba tegye a korrelációt megtalálni kívánt adatokat
Ezt a "Mentés másként" menü segítségével tehetjük meg.
Lépés 3. Nyissa meg az R Editor programot
Ha a terminálról dolgozik, futtassa az R -t. Ha az asztalon dolgozik, kattintson az R ikonra.
4. lépés. Írja be a következő parancsot:
- d <- read.csv ("NAME_OF_YOUR_CSV.csv"), és nyomja meg az Enter billentyűt.
- leadott (rang (d [, 1]), rang (d [, 2]))
Tippek
Az adatoknak legalább 5 párból kell állniuk, hogy látható legyen a trend (az adatok száma a példában csak 3 pár, a számítások egyszerűsítése érdekében.)
Figyelem
- A Spearman -rang korrelációs együtthatója csak akkor határozza meg a korreláció erősségét, ha az adatok következetesen emelkednek vagy csökkennek. Ha más tendencia mutatkozik az adatokban, Spearman rangkorrelációja nem pontos ábrázolást nyújt.
- Ez a képlet azon a feltételezésen alapul, hogy nincsenek egyenlő minősítések. Ha ugyanaz a rang, mint a példában, akkor ezt a definíciót kell használnunk: a rang szerinti szorzási momentum korrelációs együtthatója.
