- Szerző Jason Gerald [email protected].
- Public 2024-01-15 08:16.
- Utoljára módosítva 2025-01-23 12:20.
A normál erő annak az erőnek a nagysága, amely szükséges ahhoz, hogy bármely más forgatókönyvben a többi erőt semlegesítse. A megtalálás legjobb módja az objektum állapotától és a rendelkezésre álló változóktól függ. Olvasson tovább, ha többet szeretne megtudni.
Lépés
1. módszer az 5 -ből: Normál stílus nyugalomban
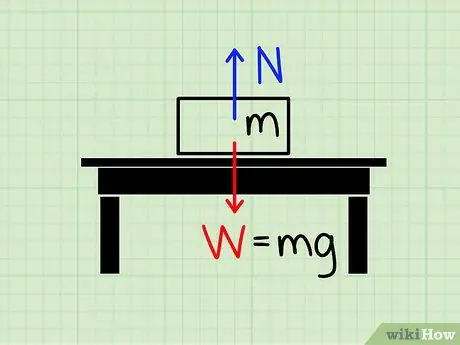
1. lépés: Értse meg a normál erő jelentését
A normál erő a gravitációs erő érvénytelenítésére használt erő nagyságát jelenti.
Képzeljünk el egy blokkot nyugalomban az asztalon. A gravitációs erő a föld felé húzza a tömböt, de egyértelmű, hogy van egy erő, amely megakadályozza, hogy a blokk összetörje az asztalt és a földre essen. Azt az erőt nevezzük, amely a gravitációs erő ellenére megállítja ezt a blokkot normális stílus.
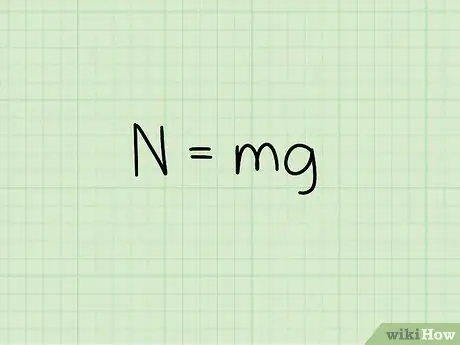
2. Lépés. Ismerje a nyugalmi állapotban lévő tárgyra gyakorolt normál erő egyenletét
Amikor kiszámítja az objektum normál erejét, amikor nyugalomban van sík felületen, használja a következő képletet: N = m * g
- Ebben az egyenletben, N a normális stílust szimbolizálja, m a tárgy tömegét jelenti, és g a gravitáció miatti gyorsulást jelenti.
- Sima felületen nyugvó, külső erőhatás nélküli tárgy esetén a normál erő megegyezik a tárgy tömegével. Ahhoz, hogy egy tárgy nyugalomban maradjon, a normál erőnek meg kell egyeznie a tárgyra ható gravitációs erővel. A tárgyra ható gravitációs erő a tárgy súlya, vagy a tárgy tömege a gravitáció miatti gyorsulás szorzata.
- Példa: Keresse meg a 4,2 kg tömegű blokk normál erejét.
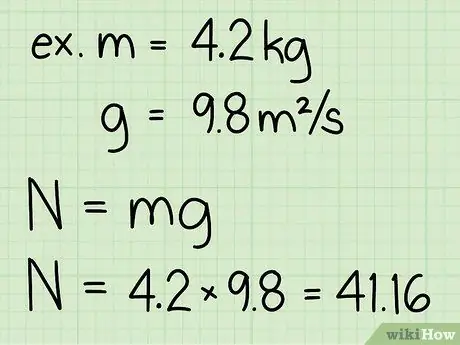
3. lépés: Szorozzuk meg a tárgy tömegét és a gravitáció miatti gyorsulást
Ez a szorzás létrehozza az objektum súlyát, amely természetesen megegyezik a nyugalmi állapotban lévő tárgy normál erejével.
- Ne feledje, hogy a gravitáció miatti gyorsulás a földfelszínen mindig állandó: g = 9,8 m/s2
- Példa: súly = m * g = 4, 2 * 9, 8 = 41, 16

4. lépés. Írja le válaszait
Az előző lépés megoldja a problémát, megadja a választ.
Példa: A normál erő 41, 16 N
2. módszer az 5 -ből: Normál erő ferde síkon
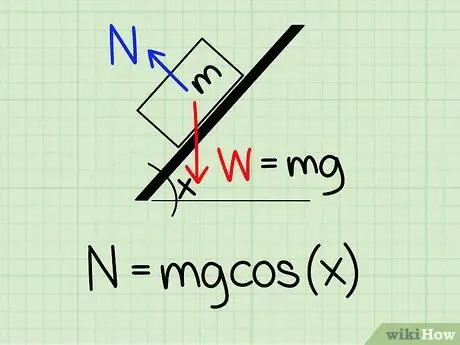
1. lépés. Használja a helyes egyenletet
A normál erő kiszámításához egy bizonyos szögben megdöntött tárgyra a következő képletet kell használnia: N = m * g * cos (x)
- Ehhez az egyenlethez, N a normális stílust szimbolizálja, m a tárgy tömegét jelenti g a gravitáció miatti gyorsulást jelenti, és x ferde szöget jelent.
- Példa: Keresse meg a 4,2 kg tömegű tömb normál erejét, amely 45 fokos dőlésszögű ferde síkon nyugszik.

2. lépés. Keresse meg a szög koszinuszát
A szög koszinusza megegyezik a komplementer szög szinuszával, vagy a szomszédos oldallal osztva a lejtés által alkotott háromszög hipotenuszával.
- Ezt az értéket gyakran számológéppel határozzák meg, mert bármely szög koszinusz mindig állandó, de manuálisan is kiszámíthatja.
- Példa: cos (45) = 0,71
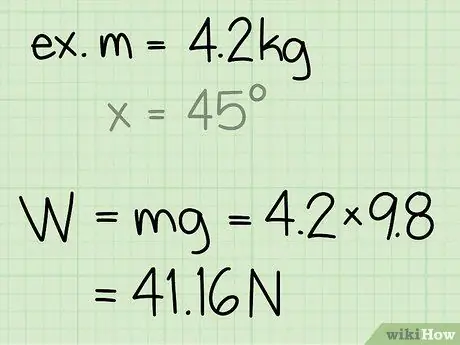
3. lépés. Keresse meg az objektum súlyát
Egy tárgy súlya megegyezik a tárgy tömegével a gravitáció miatti gyorsulással.
- Vegye figyelembe, hogy a gravitáció miatti gyorsulás a Föld felszínén mindig állandó: g = 9,8 m/s2
- Példa: súly = m * g = 4, 2 * 9, 8 = 41, 16
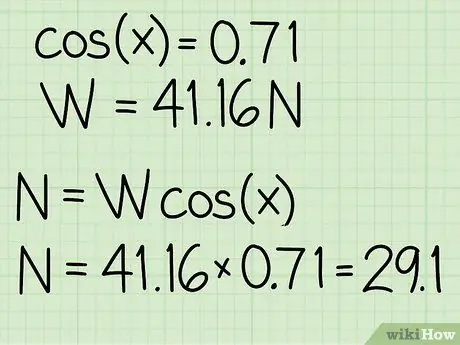
4. lépés Szorozza meg a két értéket
A normál erő megtalálásához meg kell szorozni az objektum súlyát a hajlásszög koszinuszával.
Példa: N = m * g * cos (x) = 41, 16 * 0, 71 = 29, 1
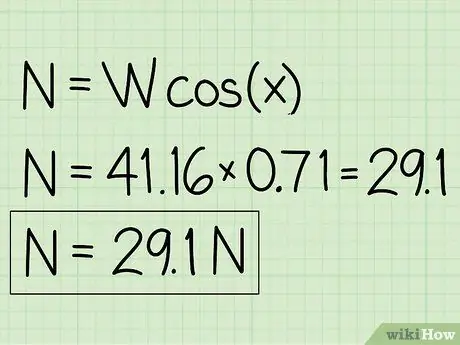
5. lépés. Írja le válaszait
Az előző lépés megoldja a problémát, és megadja a választ.
- Vegye figyelembe, hogy ha egy tárgy nyugalomban van egy lejtőn, a normál erő kisebb lesz, mint az objektum súlya.
- Példa: A normál erő 29,1 N.
3. módszer az 5 -ből: Normál stílus külső lefelé stílussal
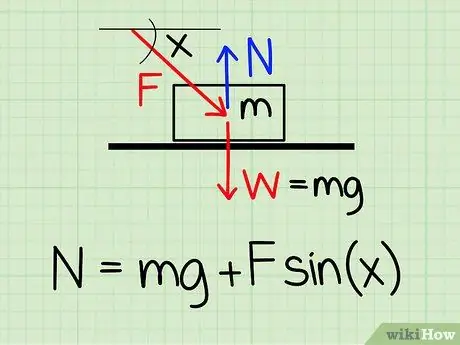
1. lépés. Használja a helyes egyenletet
A normál erő kiszámításához nyugalmi állapotban lévő objektumra, ha külső lefelé ható erő van rá, használja az alábbi egyenletet: N = m * g + F * sin (x) '
- N a normális stílust szimbolizálja, m a tárgy tömegét jelenti g a gravitáció miatti gyorsulást jelenti, F a külső stílust szimbolizálja, és x a tárgy és a külső erő iránya közötti szöget jelöli.
- Példa: Keresse meg a 4,2 kg tömegű tárgy normál erejét, ha a személyt 30 fokos szögben és 20,9 N erővel tolja.
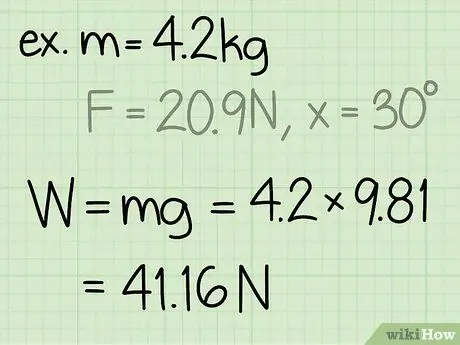
2. lépés. Keresse meg az objektum súlyát
Egy tárgy súlya megegyezik a tárgy tömegével a gravitáció miatti gyorsulással.
- Ne feledje, hogy a gravitáció miatti gyorsulás a földfelszínen mindig állandó: g = 9,8 m/s2
- Példa: súly = m * g = 4, 2 * 9, 8 = 41, 16
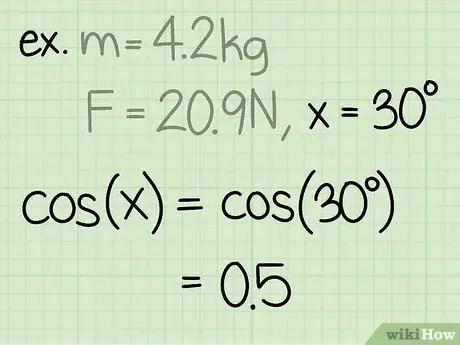
3. lépés. Keresse meg a szög szinuszát
A szög szinuszát úgy kell kiszámítani, hogy a háromszög szöggel szembeni oldalát elosztjuk a szög hipotenuszával.
Példa: sin (30) = 0,5

4. lépés Szorozza meg a szinuszt a külső erővel
A külső erő ebben a példában az objektumot érő lefelé irányuló erőre vonatkozik.
Példa: 0, 5 * 20, 9 = 10, 45
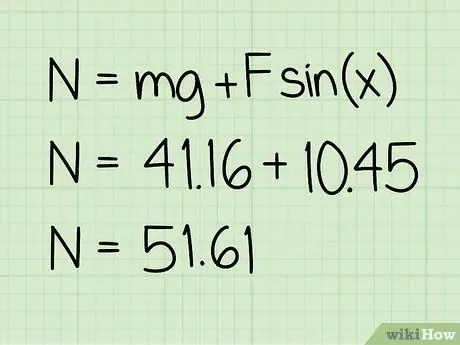
5. lépés. Adja hozzá ezt az értéket a súlyhoz
Ez az összeg megadja a normál erő nagyságát.
Példa: 10, 45 + 41, 16 = 51, 61
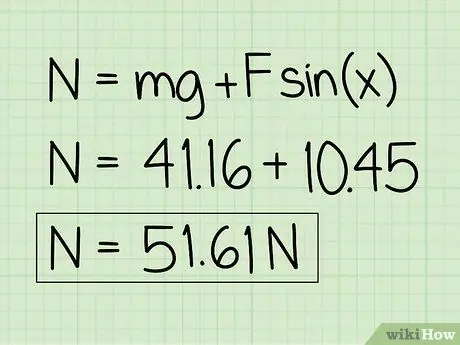
6. lépés. Írja le válaszait
Ne feledje, hogy egy nyugalmi állapotban lévő tárgyra, amelyet külső lefelé ható erő befolyásol, a normál erő nagyobb lesz, mint az objektum súlya.
Példa: A normál erő 51,61 N
4. módszer az 5 -ből: Normál stílus, külső stílus felfelé
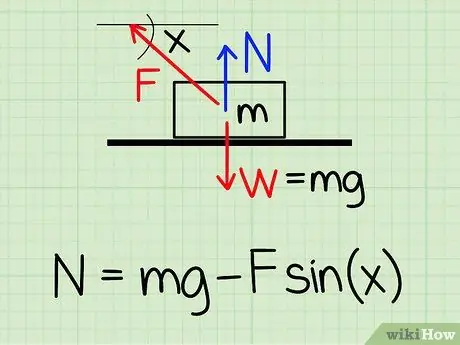
1. lépés. Használja a helyes egyenletet
A normál erő kiszámításához nyugalmi állapotban lévő objektumra, ha külső felfelé irányuló erő hat rá, használja az alábbi egyenletet: N = m * g - F * sin (x) '
- N a normális stílust szimbolizálja, m a tárgy tömegét jelenti g a gravitáció miatti gyorsulást jelenti, F a külső stílust szimbolizálja, és x a tárgy és a külső erő iránya közötti szöget jelöli.
- Példa: Keresse meg a 4,2 kg tömegű tömb normál erejét, ha valaki felhúzza a tömböt 50 fokos szögben és 20,9 N erővel.

2. lépés. Keresse meg az objektum súlyát
Egy tárgy súlya megegyezik a tárgy tömegével a gravitáció miatti gyorsulással.
- Ne feledje, hogy a gravitáció miatti gyorsulás a földfelszínen mindig állandó: g = 9,8 m/s2
- Példa: súly = m * g = 4, 2 * 9, 8 = 41, 16
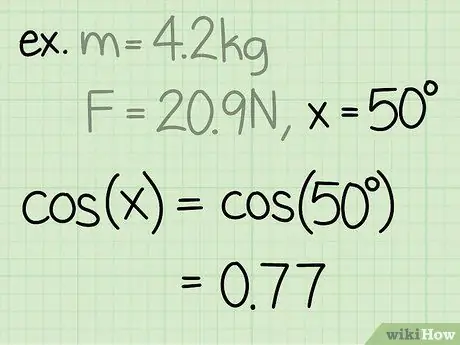
3. lépés. Keresse meg a szög szinuszát
A szög szinuszát úgy kell kiszámítani, hogy a háromszög szöggel szembeni oldalát elosztjuk a szög hipotenuszával.
Példa: sin (50) = 0, 77

4. lépés Szorozza meg a szinuszt a külső erővel
A külső erő az objektumot érő felfelé irányuló erőre utal, ebben az esetben.
Példa: 0,77 * 20, 9 = 16, 01
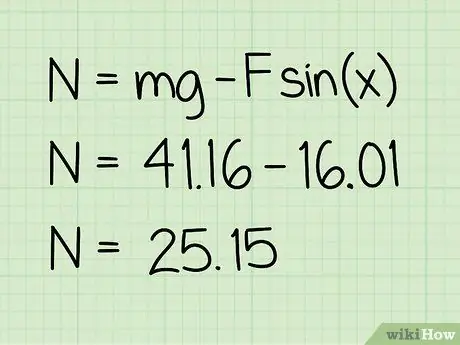
5. lépés. Vonja le ezt az értéket a súlyból
A kivonás megadja a rá ható normál erő nagyságát.
Példa: 41, 16 - 16, 01 = 25, 15
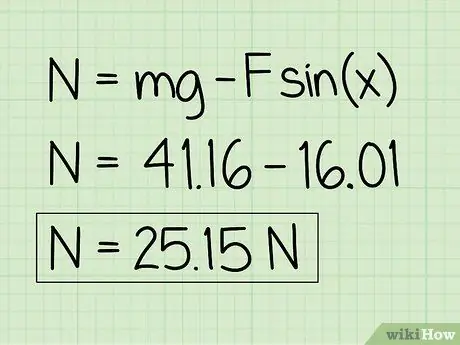
6. lépés. Írja le válaszait
Vegye figyelembe, hogy a nyugalmi állapotban lévő tárgyat felfelé irányuló külső erő befolyásolja, a normál erő kisebb lesz, mint az objektum súlya.
Példa: A normál erő 25, 15 N
5. módszer az 5 -ből: Normál erő és súrlódás

1. lépés. Ismerje a kinetikus súrlódás alapvető egyenletét
A kinetikus súrlódás vagy a mozgó tárgy súrlódása megegyezik a súrlódási együtthatóval a tárgy normál erejével. Egyenlet formájában: f = * N
- Ebben az egyenletben, f súrlódást szimbolizál, ️ a súrlódási együtthatót jelenti, és N a tárgy normál erejét jelenti.
- A "súrlódási együttható" a súrlódási erő és a normál erő aránya, amely két ellentétes felületet összenyom.
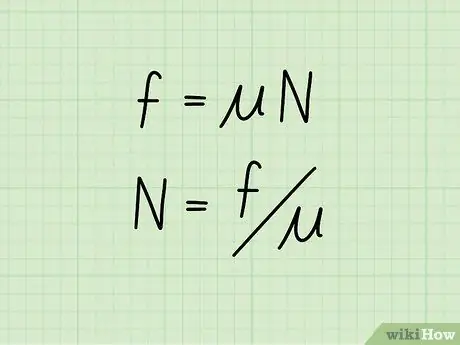
2. lépés Állítsa be az egyenletet a normál erő elkülönítésére
Ha ismeri az objektum mozgási súrlódásának értékét, valamint a súrlódási együtthatóját, a normál erőt a következő képlet segítségével számíthatja ki: N = f /
- Az eredeti egyenlet mindkét oldalát osztjuk ️, ezáltal elkülönítve az egyik oldalon a normál erőt, míg a másikon a súrlódási és mozgási súrlódási együtthatót.
- Példa: Keresse meg a blokk normális erejét, ha a súrlódási együttható 0,4 és a kinetikus súrlódás nagysága 40 N.
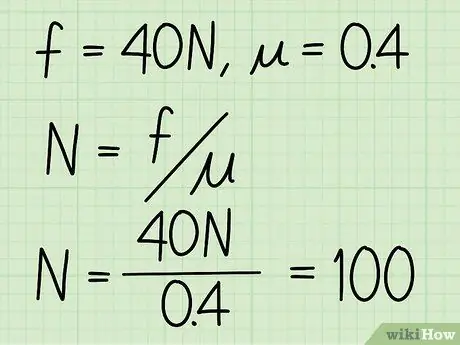
3. lépés. A kinetikus súrlódást ossza el a súrlódási együtthatóval
Alapvetően ennyit kell tennie a normál erő nagyságának megállapításához.
Példa: N = f / = 40 /0, 4 = 100
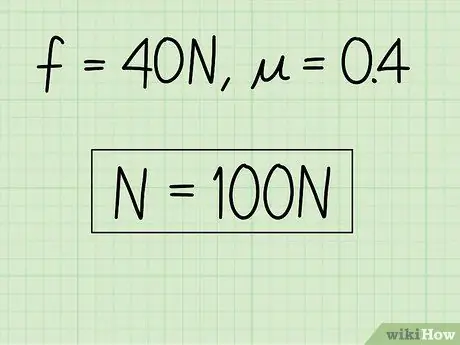
4. lépés. Írja le válaszait
Kívánt esetben ellenőrizheti válaszát, ha visszahelyezi az eredeti egyenletbe a kinetikus súrlódás szempontjából. Ha nem akarod, megoldottad a problémát.






