Amíg ismeri a másik két szög mértékét, könnyű megtalálni a háromszög harmadik szögét. Csak ki kell vonni a két szög összegét 180 fokkal. Van azonban más módszer is, amellyel megkeresheti a háromszög harmadik szögét, ha a probléma alakja kissé eltér a megszokottól. Ha tudni szeretné, hogyan találja meg a háromszög harmadik szögét, kövesse az alábbi útmutatót.
Lépés
Módszer 1 /3: A másik két szög mértékeinek használata
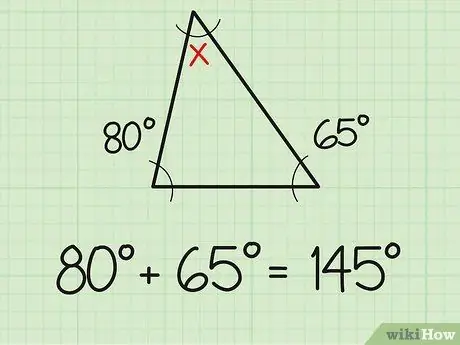
1. lépés. Adja össze a két ismert szöget
Egy tény, amit tudnia kell, hogy a háromszög három szögének összege mindig 180 fok. Tehát, ha már ismeri a háromszög két szögének mértékét, a harmadik szög megtalálása olyan egyszerű lesz, mint az egyszerű összeadás és kivonás feladata. Először is add össze a már ismert két szögmérőt. Például két ismert szög 80 és 65 fokos. Ha összeadja a kettőt (80+65), akkor 145 fokot kap.
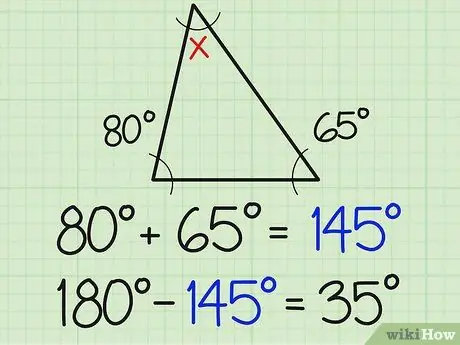
2. lépés. Oszd meg ezt a számot 180 -zal
Egy háromszög három szögének összege mindig 180 fok. Ezért a harmadik szögnek 180 -nak kell lennie, amikor hozzáadjuk a szög két ismert mértékének összegéhez. A fenti példában ez azt jelenti, hogy 180-154 = 35.
3. lépés. Írja meg válaszát
Most megvan a válasz a harmadik szögre (a példában 35 fok). Ha még mindig kétségeid vannak, nézd meg magad. Ha összeadja a három szöget, akkor 180 -as eredményt kell kapnia. Ha nem, akkor a számítás hibás. Ebben a példában 80+65+35 = 180. Ha helyes, akkor azt jelenti, hogy megoldotta a problémát.
2. módszer a 3 -ból: Változók használata
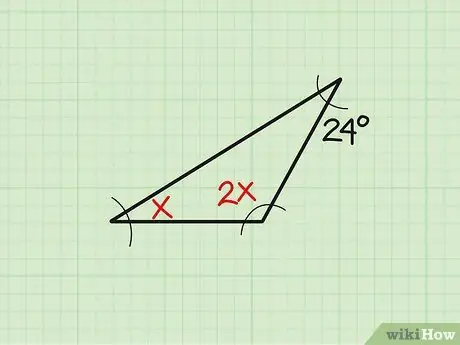
1. lépés. Írja le a problémát
Néha a meglévő szög mérete változó formában jelenik meg. Vegyük ezt a példát: „Keresse meg a háromszög„ x”szögét, ha a három szög„ x”,„ 2x”és 24 -es.” Először is írja le a problémát.
2. lépés. Adja össze az összes szögmérőt
Az elv, amire emlékeznie kell, ugyanaz marad. Tehát először összeadjuk a feladat három szögét, nevezetesen "x+2x+24 = 3x+24".
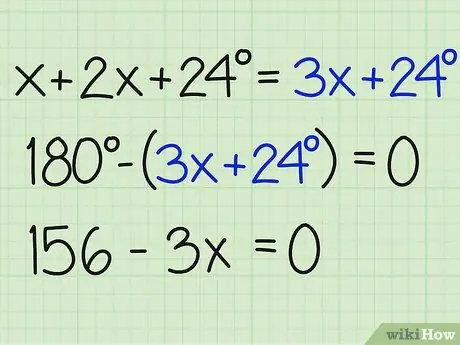
3. lépés. Oszd meg a szögek összegét 180 -mal
Most különböztesse meg ezt a számot 180 fokkal, hogy megtalálja az x -et, és megtudja a problémára adott választ. Ügyeljen arra, hogy az egyenletet nullával fejezze be. Így írják:
- 180- (3x+24) = 0
- 180-3x-24 = 0
- 156-3x = 0
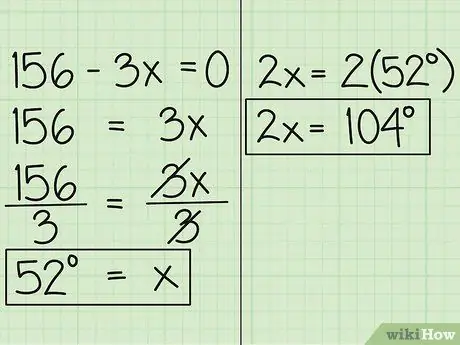
4. lépés. Keresse meg x értékét
Most helyezze a változót az egyenlet másik oldalára, és 156 = 3x lesz. Ezután ossza el az egyenletet 3 -mal, így x = 52. Ez azt jelenti, hogy a szög x -ben kifejezett mértéke 52 fok. A másik szög 2x -ben kifejezve 52 fok kétszerese, ami 104 fok.
5. lépés. Ellenőrizze az eredményeket
Ha meg akarja győződni arról, hogy a válasz helyes, egyszerűen adja hozzá a három szögmérőt, amelyekre már megtalálta a választ. Ha az eredmény 180, az azt jelenti, hogy a válasz helyes. Ebben a példában 52+104+24 = 180.
3. módszer 3 -ból: Más módszerek használata
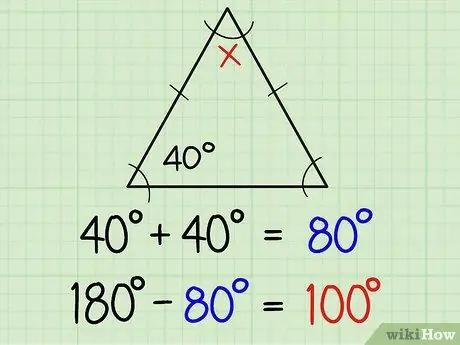
1. lépés. Keresse meg az egyenlő szárú háromszög szögeit
Egy egyenlő szárú háromszögnek két egyenlő oldala és két egyenlő szöge van. Két egyenlő oldalt általában kis vonallal jelölnek az oldalvonal közepén, ami azt jelenti, hogy a vonal két ellentétes szöge azonos mértékű. Ha már ismeri az egyik szög méretét, akkor automatikusan ismeri a másik szöget is. Itt további magyarázat:
Ha az egyik egyenlő szög 40 fok, akkor a másik 40 fok. Így megtalálhatja mind a három szöget a 40+40 (azaz 80) és a 180, vagyis 180-80 = 100 összeg közötti különbséggel
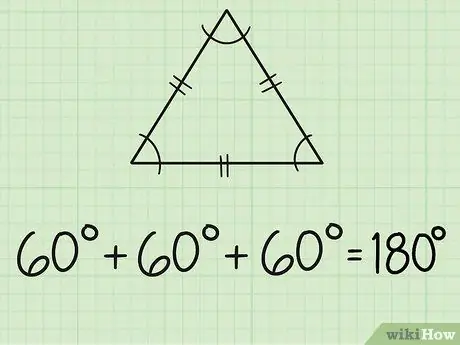
2. lépés. Keresse meg az egyenlő oldalú háromszög szögeit
Egy egyenlő oldalú háromszögnek három egyenlő oldala és három egyenlő szöge van. Mindegyik oldalt általában két rövid vonallal jelölik a közepén. Mivel mindhárom szög egyenlő, ez azt jelenti, hogy minden szög 60 fokos, mert 180/3 = 60.
3. lépés. Keresse meg a derékszögű háromszög harmadik szögét
Tegyük fel, hogy derékszögű háromszöget kapunk, az egyik hegyesszög 30 fokos. Mivel a háromszög derékszög, ez azt jelenti, hogy az egyik szögnek, nevezetesen a derékszögnek 90 fokosnak kell lennie. Ezután használja a háromszög elvet, a két szög (90+30 = 120) összege közötti különbség 180-szor, akkor 180-120 = 60 fokot kap.
