A rombusz négyszög, négy egyenlő oldalával. Három képlet létezik a rombusz területének megkeresésére. Csak kövesse ezeket a lépéseket, hogy megtudja, hogyan.
Lépés
Módszer 1 /3: Átlós használata
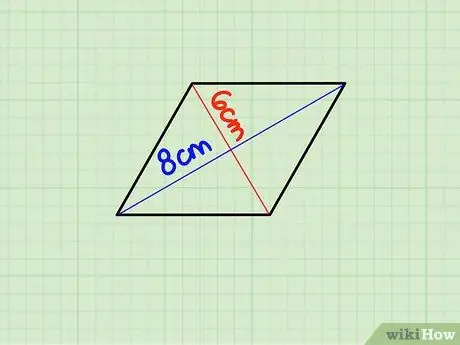
1. lépés. Keresse meg az egyes átlók hosszát
A rombusz átlói az alakzat közepén egymással szemben lévő csúcsokat (sarkokat) összekötő vonalak. A rombusz átlói merőlegesek és négy derékszögű háromszöget alkotnak a metszésponton keresztül.
Tegyük fel, hogy az átló 6 cm, a hossza 8 cm
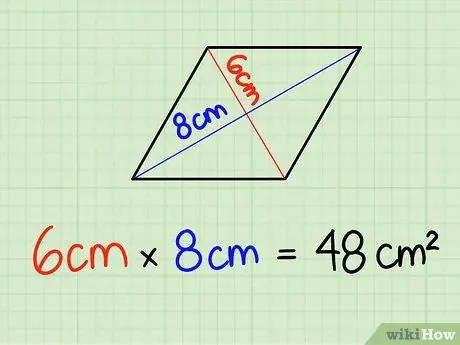
2. lépés: Szorozzuk meg az átló hosszát
Csak írja le az átló hosszát és szorozza meg. Ebben az esetben 6 cm x 8 cm = 48 cm2. Ne felejtse el megszorozni az egységeket, mert négyzet alakú egységekkel dolgozunk.
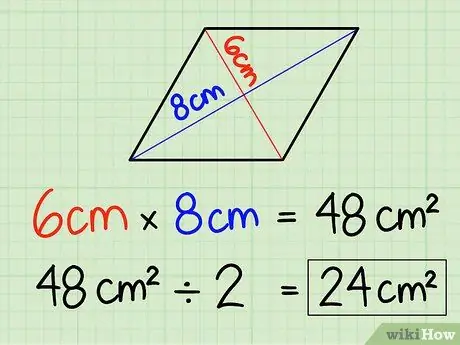
3. lépés. Oszd meg az eredményt 2 -vel
Mert 6 cm x 8 cm = 48 cm2, csak ossza el az eredményt 2,48 cm -rel2/2 = 24 cm2. A rombusz területe 24 cm2.
2. módszer a 3 -ból: Az alap és a magasság használata
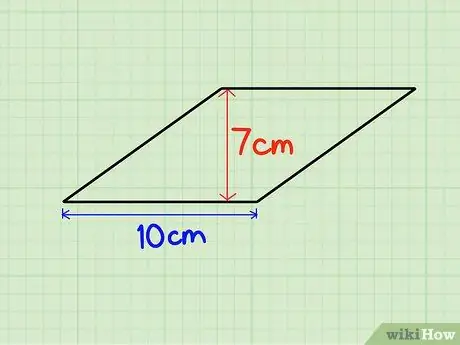
1. lépés. Keresse meg az alapot és a magasságot
A rombusz magasságát megszorozhatjuk a rombusz oldalának hosszával is. Tegyük fel, hogy a rombusz magassága 7 cm, az alapja 10 cm.
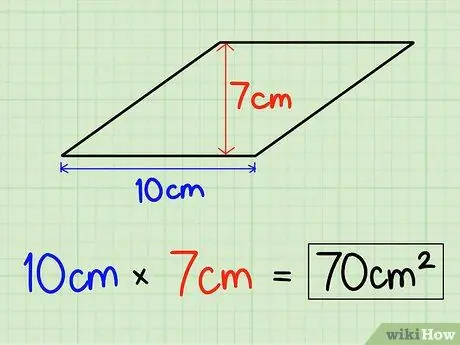
2. lépés Szorozza meg az alapot és a magasságot
Miután megtudta a rombusz alapját és magasságát, keresse meg az alakzat területét úgy, hogy megszorozza. Tehát 10 cm x 7 cm = 70 cm2. A rombusz területe 70 cm2.
3. módszer 3 -ból: Trigonometria használata
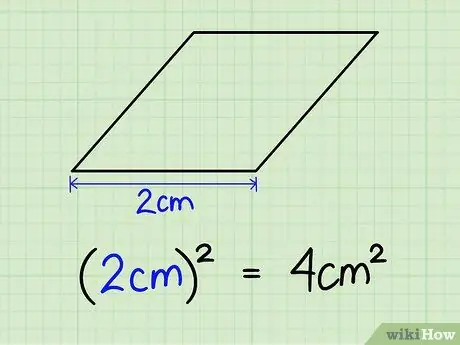
1. lépés Négyzetesítse ki bármelyik oldal hosszát
Egy rombusznak négy egyenlő oldala van, így nem mindegy, hogy melyik oldalt választjuk. Tegyük fel, hogy az oldal hossza 2 cm. 2 cm x 2 cm = 4 cm2.
2. lépés: Szorozzuk meg az egyik sarok szinuszával
Nem mindegy, hogy melyik szöget választjuk. Tegyük fel, hogy az egyik szög 33 fok. Csak szorozza meg a szinuszt (33) 4 cm -rel2 hogy megkapja a rombusz területét. (2 cm)2 x szinusz (33) = 4 cm2 x 1 = 4 cm2. A rombusz területe 4 cm2.
