Nem tudja, hogyan kell lineáris egyenleteket rajzolni számológép használata nélkül? Szerencsére a lineáris egyenletek ábrázolása meglehetősen egyszerű, ha tudja, hogyan. Mindössze annyit kell tennie, hogy megért néhány dolgot az egyenletéről, és képes lesz rá. Kezdjük.
Lépés
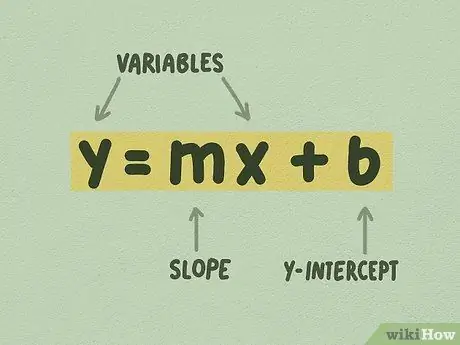
1. lépés. Győződjön meg arról, hogy a lineáris egyenlet formája y = mx + b
Ezt az alakzatot y-metsző alaknak nevezik, és valószínűleg ez a legegyszerűbb forma a lineáris egyenletek grafikálására. Az egyenletben szereplő értéknek nem kell egész számnak lennie. Gyakran előfordul, hogy a következőképpen néz ki egy egyenlet: y = 1/4x + 5, ahol 1/4 m, 5 pedig b.
- m -t "lejtésnek", vagy néha "gradiensnek" nevezik. A meredekség az oldal feletti növekedés, vagy az y változása osztva az x változásával.
- b az "y-elfogás". Az y-metszés az a pont, ahol az egyenes metszi az Y tengelyt.
- x és y változók. Megoldhat egy adott x értéket, például, ha van y pontja, és ismeri az m és b értékét. Azonban az x -nek soha nincs csak egy értéke: értéke változik, ahogy a sor felfelé vagy lefelé halad.
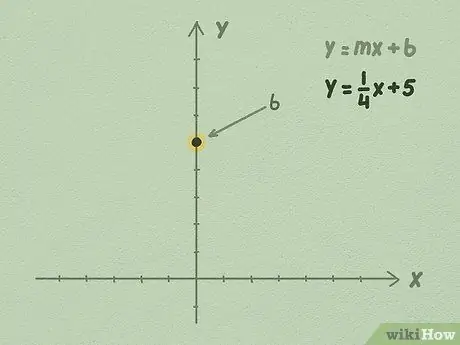
2. lépés. Rajzolja fel a b számot az Y tengelyen
A b értéke mindig racionális szám lesz. Bármi legyen is a b szám, keresse meg az értékét az Y tengelyen, és helyezze a számot a függőleges tengely egy pontjára.
Például használjuk az y = 1/4x + 5 egyenletet. Mivel az utolsó szám b, tudjuk, hogy b egyenlő 5. Mozogjon felfelé 5 ponttal az Y tengelyen, és jelölje meg a pontokat. Itt az egyenes metszi az Y tengelyt
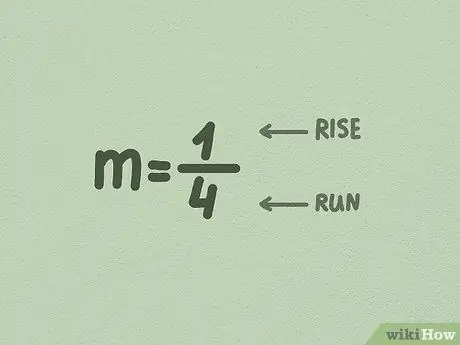
Lépés 3. Az m -t alakítsa törtre
Gyakran előfordul, hogy az x előtti szám már töredék, így nem kell módosítania. De ha nem, akkor csak módosítsa úgy, hogy az m értékét az 1 -es szám alá helyezi.
- Az első szám (a számláló) a növekmény növekedése osztva az oldallal. Ez a szám azt jelzi, hogy a vonal meddig megy felfelé vagy függőlegesen.
- A második szám (nevező) a növekvő oldal osztva az oldallal. Ez a szám azt jelzi, hogy a vonal milyen mértékben mozog oldalirányban vagy vízszintesen.
- Például:
- A 4/1 meredekség 4 pontot mozgat felfelé minden 1 pontra oldalra.
- A -2/1 meredekség 2 pontot mozgat lefelé minden 1 pontért oldalra.
- Az 1/5 -ös meredekség 1 pontot felfelé mozgat minden 5 pontra oldalra.
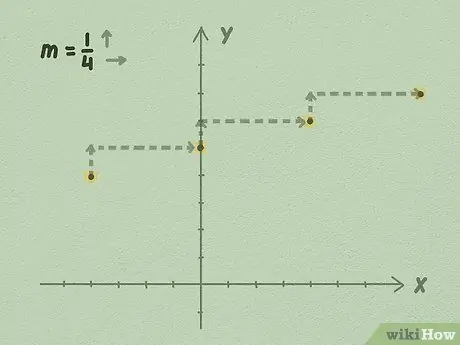
4. lépés: A vonal b -ből való kiterjesztése a lejtő segítségével, vagy felfelé osztva az oldallal
Kezdje a b értékével: tudjuk, hogy az egyenlet ezen a ponton túlmegy. Hosszabbítsa meg az egyenest úgy, hogy felveszi a meredekségét, és annak értékét használva kapja meg az egyenlet pontjait.
- Például a fenti ábra segítségével láthatja, hogy minden 1 ponttal felfelé a vonal 4 pontot mozgat jobbra. Ez azért történik, mert a vonal meredeksége 1/4. A vonalat korlátlanul meghosszabbítja mindkét oldalra, továbbra is az oldalt felosztva használja fel a vonal ábrázolásához.
- A lejtés pozitív, ha felfelé halad, míg a lejtés negatív, amikor lefelé mozog. Például, ha a lejtés -1/4, akkor minden 4 pont oldalirányban 1 ponttal lejjebb kerül.
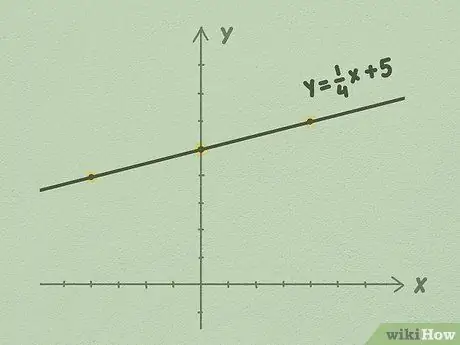
Lépés 5. Folytassa a vonal kiterjesztését vonalzó segítségével, és ügyeljen arra, hogy az m lejtést iránymutatóként használja
Hosszabbítsa meg a sort a végtelenségig, és készen áll a lineáris egyenlet ábrázolására. Elég könnyű, igaz?
