A mátrix a számok, szimbólumok vagy kifejezések téglalap alakú elrendezése sorokban és oszlopokban. A mátrix megszorzásához meg kell szorozni a mátrix első sorában lévő elemeket (vagy számokat) a mátrix második sorának elemeivel, és össze kell adni a szorzatot. A mátrixokat csak néhány egyszerű lépéssel szorozhatja meg, amelyek megkövetelik az eredmények helyes összeadását, szorzását és elhelyezését.
Lépés
1. lépés. Győződjön meg arról, hogy a mátrixok megsokszorozhatók
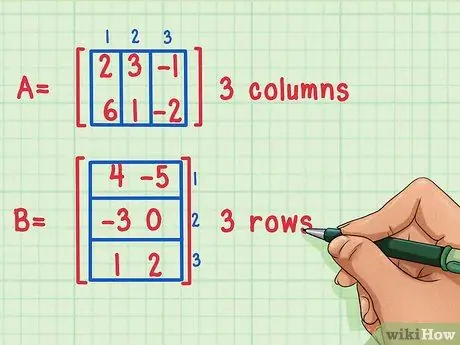
Csak akkor szaporíthat mátrixot, ha az első mátrix oszlopainak száma megegyezik a második mátrix sorainak számával.
Ezeket a mátrixokat meg lehet szorozni, mert az első mátrixnak, az A mátrixnak 3 oszlopa van, míg a második mátrixnak, a B mátrixnak 3 sora van
2. lépés Jelölje meg a mátrixtermék méreteit
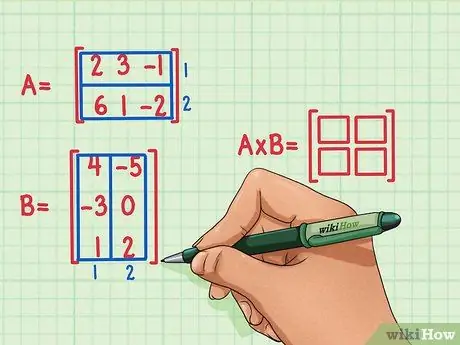
Hozzon létre egy új, üres mátrixot, amely jelzi a két mátrix szorzatának méreteit. Az A és B mátrix szorzatát reprezentáló mátrixnak ugyanannyi sora lesz, mint az első mátrixnak, és ugyanannyi oszlopa lesz, mint a második mátrixnak. Rajzolhat üres mezőket a mátrix sorainak és oszlopainak számának megjelenítéséhez.
- Az A mátrixnak 2 sora van, tehát a mátrix szorzásának eredménye 2 sor lesz.
- A B mátrixnak 2 oszlopa van, tehát a mátrix szorzásának eredménye 2 oszlopból áll.
- A mátrixtermék eredménye 2 sor és 2 oszlop lesz.
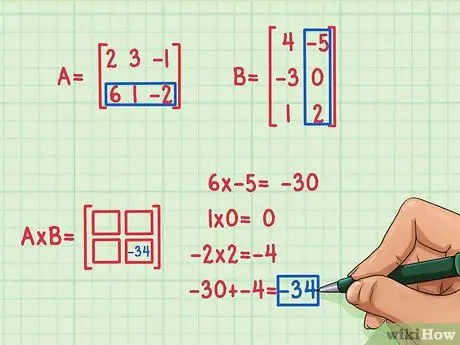
3. lépés. Keresse meg az első pont termék eredményét
Az első ponttermék eredményének megtalálásához meg kell szorozni az első sor első elemét az első oszlop első elemével, az első sor második elemét az első oszlop második elemével és a harmadik elemet a az első sort az első oszlop harmadik elemével. Ezután össze kell adnia a szorzási eredményeket pont termék (pont).
Tegyük fel, hogy először úgy dönt, hogy kiszámítja a mátrix szorzat második sorában és második oszlopában (jobb alsó sarokban) található elemeket. Ezt tegye a következőképpen:
- 6 x -5 = -30
- 1 x 0 = 0
- -2 x 2 = -4
- -30 + 0 + (-4) = -34
-
A pontozott termék eredménye -34, és ezt az eredményt a mátrixtermék jobb alsó sarkába írják.
Amikor egy mátrixot megszoroz, a pontszorzat az első mátrix sorhelyébe és a második mátrix oszloppozíciójába kerül. Például, ha ismeri az A mátrix alsó sorának ponttermékét és a B mátrix jobb oszlopát, a válasz, -34, a mátrix szorzat alsó sorába és jobb oszlopába íródik
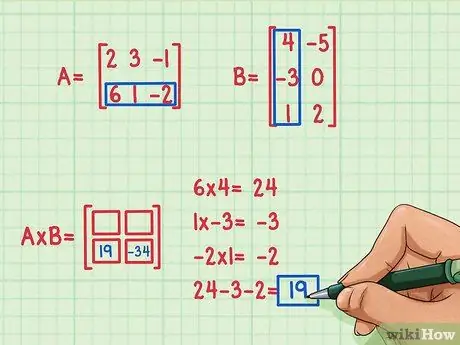
4. lépés Keresse meg a második pont termék eredményét
Tegyük fel, hogy a kifejezést a mátrixtermék bal alsó sarkában szeretné megtalálni. Ennek a kifejezésnek a megtalálásához csak meg kell szoroznia az első mátrix alsó sorában lévő elemeket a második mátrix első oszlopának elemeivel, majd össze kell adnia őket. Használja ugyanazt a módszert, mint az első sor és oszlop megszorzása - keresse újra pont termék (nem t) övé.
- 6 x 4 = 24
- 1 x (-3) = -3
- (-2) x 1 = -2
- 24 + (-3) + (-2) = 19
- A pontozott termék eredménye -19, és ezt az eredményt a mátrixtermék bal alsó sarkába írják.
5. lépés Keresse meg a másik két pontos terméket
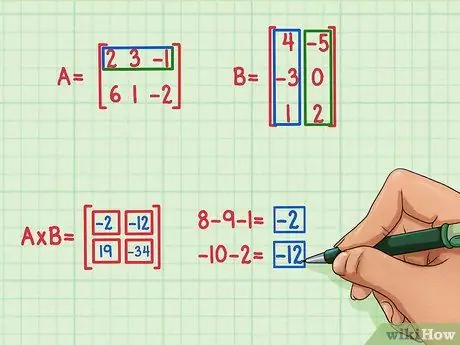
Ha meg szeretné találni a kifejezést a mátrixtermék bal felső sarkában, először keresse meg az A mátrix felső sorának és a B mátrix bal oszlopának ponttermékét.
- 2 x 4 = 8
- 3 x (-3) = -9
- (-1) x 1 = -1
- 8 + (-9) + (-1) = -2
-
A pontozott termék eredménye -2, és ezt az eredményt a mátrixtermék bal felső sarkába írják.
Ha meg szeretné találni a kifejezést a mátrixtermék jobb felső sarkában, keresse meg az A mátrix felső sorának és a B mátrix jobb oszlopának ponttermékét
- 2 x (-5) = -10
- 3 x 0 = 0
- (-1) x 2 = -2
- -10 + 0 + (-2) = -12
- A pont szorzat -12, és ezt az eredményt a mátrixtermék jobb felső sarkában írják fel.
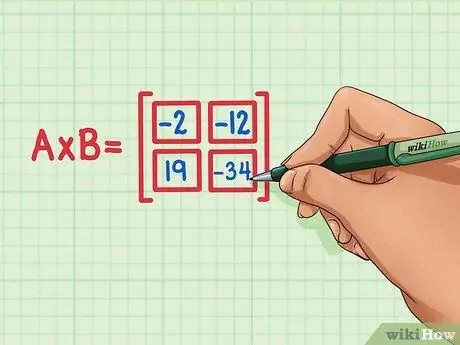
6. lépés. Győződjön meg arról, hogy a négypontos termék a megfelelő helyen van a mátrixtermékben
A 19 -nek a bal alsó sarokban kell lennie, a -34 -nek a jobb alsó sarokban, a -2 -nek a bal felső sarokban kell lennie, és a -12 -nek a jobb felső sarokban kell lennie.
Tippek
- Ha a vonalszakaszokat használja, és nem használja a vonalakat, akkor rossz választ adhat. Ha egy sort reprezentáló egyeneshez hosszabbításra van szükség az oszlop átlépéséhez, akkor hosszabbítsa meg! Ez csak egy vizualizációs technika, amely megkönnyíti, hogy megtudja, mely sorokat és oszlopokat kell használni a termék egyes elemeivel való munkához.
- A két mátrix szorzata az első mátrix sorainak és a második mátrix oszlopainak számának megfelelő sorok számát adja ki.
- Írja le az összegét. A mátrixok megszorzása sok számítást foglal magában, és nagyon könnyű félrelépni, és elfelejteni, melyik számot szorozzuk.
