Az objektív nagyításának kiszámítása: 12 lépés (képekkel)

2024 Szerző: Jason Gerald | [email protected]. Utoljára módosítva: 2024-01-16 19:34

Az optikai műszerek tanulmányozása során a lencseszerű tárgy "nagyítása" a látható kép magasságának és a tárgy tényleges magasságának aránya. Például egy olyan objektívnek, amely nagyon nagynak tud kinézni egy tárgyat, "nagy" nagyítási tényezője van, míg egy objektumnak, amely kicsi megjelenést kölcsönöz, "kis" nagyítási tényezője van. Az objektum nagyításának képletét általában a képlet segítségével számítják ki M = (h_én/h_o) = -(d_én/d_o), ahol M = nagyítás, h_én = kép magassága, h_o = a tárgy magassága és d_én és D._o = a kép és a tárgy távolsága.

Lépés

1 /2 -es módszer: Egylencsés nagyítás kiszámítása

Megjegyzések: A. konvergáló lencse szélesebb a közepén, mint a szélein (mint egy nagyító). a divergens lencse szélesebb a széleken, mint a közepén (mint egy tál). A nagyítás kiszámítása mindkét lencsén ugyanaz, a egy fontos kivétel. Ide kattintva közvetlenül a divergens lencsékre vonatkozó kivételekhez juthat.

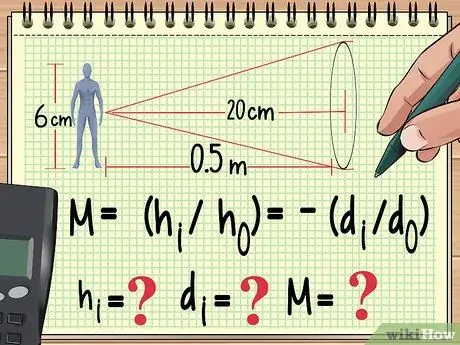
1. lépés: Kezdje egyenletével és a már ismert változókkal

Csakúgy, mint bármely más fizikai feladat, a kibővítési probléma megoldásának módja az, hogy leírja a számításhoz használt egyenletet. Innentől kezdve visszamenőleg megkeresheti annak a változónak az értékét, amelyet nem talált a használt egyenletből.

• Tegyük fel például, hogy egy 6 cm magas babát helyeznek el egy méterre a konvergáló lencse 20 cm -es gyújtótávolsággal. Ha ki akarjuk számítani a nagyítást, a képmagasságot és a kép távolságát, akkor a következőképpen kezdhetjük írni egyenletünket:

  M = (h_én/h_o) = -(d_én/d_o)

• Most már tudjuk, h_o (a baba magassága) és d_o (a baba távolsága a lencsétől). Ismerjük a lencse gyújtótávolságát is, ami ebben az egyenletben nincs. Számolni fogunk h_én, d_én, és M.

2. lépés: A lencseegyenlet segítségével d_én.

Ha ismeri a nagyítandó objektumtól való távolságot és a lencse gyújtótávolságát, a kialakított képtől való távolság kiszámítása nagyon egyszerű az objektív egyenletével. A lencse egyenlete az 1/f = 1/d_o + 1/d_én, ahol f = a lencse gyújtótávolsága.

• Ebben a példaproblémában a lencseegyenletet használhatjuk a d kiszámításához_én. Adja meg f és d értékét_én majd oldd meg az egyenletet:

  1/f = 1/d_o + 1/d_én

  1/20 = 1/50 + 1/d_én

  5/100 - 2/100 = 1/d_én

  3/100 = 1/d_én

  100/3 = d_én = 33,3 cm

• A lencse fókusztávolsága a lencse középpontjától a fény fókuszpontján áthaladó távolság. Ha valaha nagyítóval összpontosította a fényt az égő hangyákra, látta. A lecke kérdéseiben általában ennek a hotspotnak a nagyságát adtuk meg. A való életben ezeket a specifikációkat általában az objektíven elhelyezett címkére írják.

3. lépés: h kiszámítása_én.

Miután kiszámította d_o és D._én, kiszámíthatja a nagyított tárgy magasságát és a lencse nagyítását. Figyelje meg a két egyenlőjelet a lencse nagyítási egyenletében (M = (h_én/h_o) = -(d_én/d_o)) - ez azt jelenti, hogy ennek az egyenletnek minden része egyenlő egymással, így kiszámíthatjuk az M és a h értékeket_én bármilyen sorrendben akarjuk.

• Ebben a példaproblémában kiszámíthatjuk a h értéket_én mint ez:

  (h_én/h_o) = -(d_én/d_o)

  (h_én/6) = -(33, 3/50)

  h_én = -(33, 3/50) x 6

  h_én = - 3, 996 cm

• Vegye figyelembe, hogy az objektum magassága itt negatív, ami azt jelzi, hogy a később látott kép megfordul (felülről lefelé).

4. lépés: M. kiszámítása

Az utolsó változót a (-d_én/d_o) vagy (h_én/h_o).

• A következő példában az M kiszámításának módja a következő:

  M = (h_én/h_o)

  M = (-3, 996/6) = - 0, 666

• Az eredmény ugyanaz lesz, ha a d értékét használjuk:

  M = -(d_én/d_o)

  M = -(33, 3/50) = - 0, 666

• Vegye figyelembe, hogy a zoom nem rendelkezik egységcímkével.

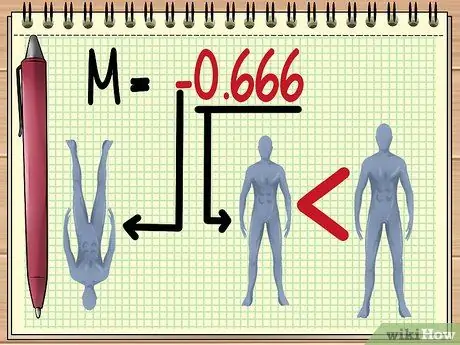
5. lépés: Az M érték megértése

Miután megkapta az M érték nagyságát, számos dolgot megbecsülhet a lencsén keresztül látható képről, nevezetesen:

• A méret.

  Minél nagyobb az M "abszolút értéke", annál nagyobb objektív jelenik meg az objektívvel. A 0 és 1 közötti M érték azt jelzi, hogy az objektum kisebbnek tűnik.

• Tárgy orientáció.

  A negatív érték azt jelzi, hogy a kialakított kép megfordul.

• Az itt megadott példában a -0,666 M érték azt jelenti, hogy a meglévő változó értéke szerint a baba árnyéka látható lesz. fejjel lefelé, és kétharmaddal kisebb, mint a tényleges méret.

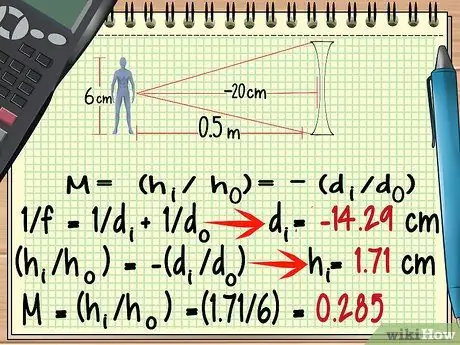
6. lépés. Változó lencsék esetén használjon negatív fókuszpontot

Bár a szétágazó lencse alakja nagyon különbözik a konvergáló lencsétől, a nagyítást a fenti képlettel lehet kiszámítani. A kivételek, amelyeket szem előtt kell tartani A szétágazó lencse fókuszpontja negatív.

A fenti példaproblémában ez befolyásolja a d számításakor kapott választ_én, ezért feltétlenül figyeljen erre.

• Feldolgozzuk a fenti példaproblémát, csak most használunk eltérõ lencsét, gyújtótávolsággal - 20 cm.

  A többi változó ugyanaz marad.

• Először is kiszámítjuk a d_én a lencsegyenlet segítségével:

  1/f = 1/d_o + 1/d_én

  1/-20 = 1/50 + 1/d_én

  -5/100 - 2/100 = 1/nap_én

  -7/100 = 1/nap_én

  -100/7 = d_én = - 14, 29 cm

• Most kiszámoljuk, h_én és M d értékkel_én az új.

  (h_én/h_o) = -(d_én/d_o)

  (h_én/6) = -(-14, 29/50)

  h_én = -(-14, 29/50) x 6

  h_én = 1,71 cm

  M = (h_én/h_o)

  M = (1, 71/6) = 0, 285

2. módszer 2 -ből: Több objektív nagyításának kiszámítása

Egyszerű kétlencsés módszer

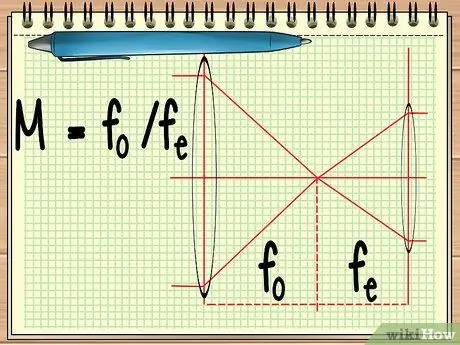
1. lépés Számítsa ki a két lencse fókuszpontját

Ha olyan műszert használ, amely két egymás mellé helyezett lencséből áll (például távcső vagy egy távcső), akkor csak a két lencse fókuszpontját kell megtudnia a két lencse teljes nagyításának kiszámításához. ezt az M = f egyszerű egyenlettel lehet kiszámítani_of_e.

Az egyenletben f_o az objektív fókuszpontja és f_e a szemlencse fókuszpontja. Az objektív lencse a nagy lencse, amely közel van a tárgyhoz, míg a szemlencse az a lencse, amely a megfigyelő szeme közelében található.

2. lépés Csatlakoztassa a már meglévő információkat az M = f egyenletbe_of_e.

Ha megvan mindkét lencse fókuszpontja, nagyon könnyű kiszámítani őket, - számítsa ki az arányt úgy, hogy elosztja az objektív fókusztávolságát a szemlencse gyújtótávolságával. A válasz az eszköz teljes nagyítása.

• Tegyük fel például, hogy egy egyszerű távcsővel azt írják, hogy az objektív fókuszpontja 10 cm, a szemlencse fókuszpontja 5 cm, akkor a nagyítás 10/5 = 2.

Bonyolult módszer

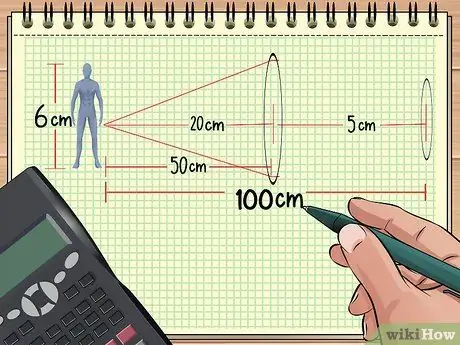
1. lépés. Számítsa ki a lencsék és a tárgy közötti távolságot

Ha két objektív van sorban elrendezve egy objektum előtt, akkor a teljes nagyítás kiszámítható, ha ismeri a lencsék és a tárgy közötti távolságot, az objektum méretét és a két lencse fókuszpontját. A maradék is kiszámítható.

Tegyük fel például, hogy tárgyakat és lencséket rendezünk a fenti 1. példában leírtak szerint: egy baba 50 cm -re van a 20 cm -es gyújtótávolságú konvergáló lencsétől. Most helyezze a második lencsét, amelynek gyújtópontja 5 cm, az első lencsétől 50 cm távolságra (100 cm -re a babától.) Ezt követően kiszámítjuk a teljes nagyítást a kapott információk felhasználásával

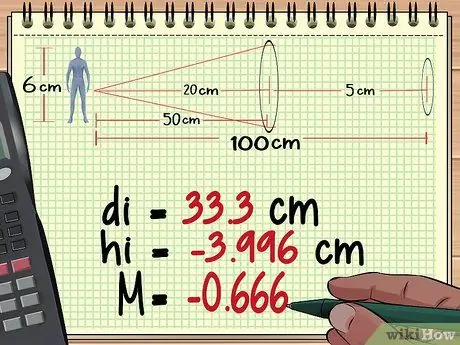
2. lépés Számítsa ki az objektív távolságát, magasságát és nagyítását az 1. lencséből

A több lencse nagyításának kiszámításának első része ugyanaz, mint egyetlen lencse nagyításának kiszámítása. Kezdje a tárgyhoz legközelebb eső lencsével, használja a lencsegyenletet a kialakított képtől való távolság meghatározásához, majd a nagyítási egyenlet segítségével keresse meg a kép magasságát és nagyítását. Kattintson ide, ha további egylencsés nagyítási számításokat szeretne megtekinteni.

• A fenti 1. módszerrel végzett számításainkból azt találjuk, hogy az első lencse olyan magas képet állít elő - 3, 996 cm, távolság 33,3 cm az objektív mögött, és nagyítással - 0, 666.

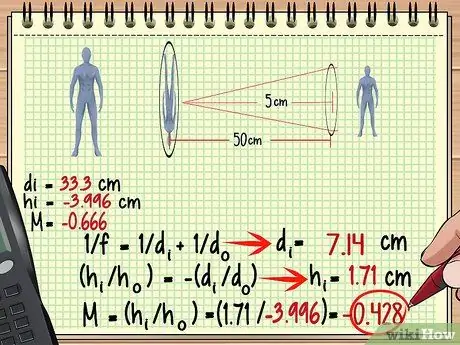
Lépés 3. Használja az első lencse képét a második lencse tárgyaként

Most nagyon könnyű megtalálni a második lencse nagyítását, magasságát és még sok mást - használja ugyanazt a módszert, amelyet az első lencséhez használt, ezúttal csak tárgyként kezelje a képet. Ne feledje, hogy a kép távolsága a második lencsétől nem mindig azonos az objektum távolságával az első lencsével.

• A fenti példában, mivel a kép 33,3 cm-rel alakul ki az első lencse mögött, a távolság 50-33,3 = 16,7 cm a második lencse előtt. Használja ezt a mérést és a második lencse gyújtótávolságát a második lencse által alkotott kép megkereséséhez.

  1/f = 1/d_o + 1/d_én

  1/5 = 1/16, 7 + 1/d_én

  0, 2 - 0, 0599 = 1/d_én

  0, 14 = 1/nap_én

  d_én = 7,14 cm

• Most kiszámíthatjuk, h_én és M a második lencséhez:

  (h_én/h_o) = -(d_én/d_o)

  (h_én/-3, 996) = -(7, 14/16, 7)

  h_én = -(0, 427) x -3, 996

  h_én = 1,71 cm

  M = (h_én/h_o)

  M = (1, 71/-3, 996) = - 0, 428

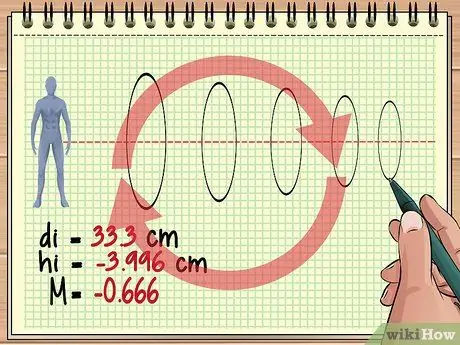
Lépés 4. Folytassa a számítást a további lencsék esetében

Ez az alapvető megközelítés ugyanaz, ha három, négy vagy száz lencse sorakozik egy tárgy előtt. Minden objektív esetében tekintse az előző lencse képét objektumnak, és használja a lencseegyenletet és a nagyítási egyenletet a kívánt válasz megtalálásához.

Ne feledje, hogy minden következő lencse folyamatosan megfordíthatja a kialakult képet. Például a korábban kapott nagyítási érték (-0, 428) azt jelzi, hogy a kép, amelyet látni fogunk, körülbelül a tényleges objektumméret 4/10 része, de merőleges, mert az előző lencse képe fordított

Tippek

• A távcső általában magyarázatot ad a nagyítási előírásokra, egy másik szám szorzatában. Például a távcső megadható 8x25 vagy 8x40 méretben. Ha így írjuk, az első szám a távcső nagyítása. Még akkor sem számít, ha a megadott példában a két szám nagyságrendje eltérő, mindkét távcső 8 -szoros nagyítású. A második szám azt jelzi, hogy milyen tiszta lesz a kép a távcsővel.
• Ne feledje, hogy egylencsés nagyító esetén a nagyítás negatív lesz, ha a tárgy távolsága nagyobb, mint az objektív gyújtótávolsága. Ez nem jelenti azt, hogy a kialakult kép kisebb lesz. Ebben az esetben a nagyítás még mindig megtörténik, de a kialakult képet fejjel lefelé (felülről lefelé) fogja látni a megfigyelő.