- Szerző Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:13.
- Utoljára módosítva 2025-01-23 12:20.
Az átlagos sebesség kiszámításához mindössze a teljes elmozdulás szükséges. vagy pozícióváltás, és a teljes idő. Ne feledje, hogy a sebesség kiszámítja az objektum irányát és sebességét is, ezért a válaszban szerepeltessen egy irányt, például "észak", "elöl" vagy "bal". Ha a sebességszámítási problémája állandó gyorsulást is magában foglal, megtanulhat egy gyors módszert arra, hogy még könnyebben megtalálja a választ.
Lépés
1 /2 -es módszer: Az elmozdulás és az idő átlagos sebességének kiszámítása

1. lépés. Ne feledje, hogy a sebesség magában foglalja a tárgy sebességét és irányát is
A sebesség azt a sebességet írja le, amellyel az objektum helyzete változik. Ennek nemcsak az objektum sebességével kell összefüggnie, hanem az irányával is. "100 méter másodpercenként dél felé" más sebességérték, mint a "100 méter másodpercenként keletre".
- Az irányított mennyiségeket vektormennyiségeknek nevezzük. Ezt a mennyiséget meg lehet különböztetni a skalármennyiségnek nevezett iránytalan mennyiségtől, ha egy nyilat írunk a változó fölé. Például a v jelölés az arányt jelenti, míg a v jelölés → sebességet vagy sebességet + irányt jelent. A cikkben használt v jelölés a sebességet jelöli.
- Tudományos problémák esetén mérőeszközöket vagy más mértékegységeket kell használni a távolság kifejezésére, míg mindennapi célokra bármilyen tetszőleges egységet használhat.
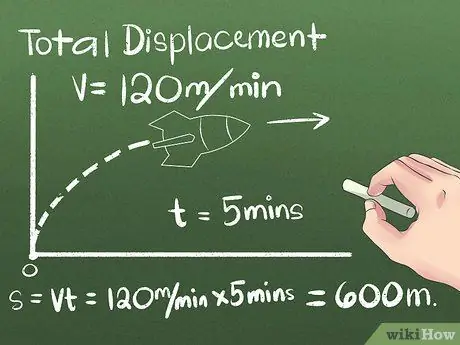
2. lépés. Keresse meg a teljes elmozdulási értéket
Az elmozdulás az objektum helyzetének változása, vagy a kezdő és a végpont közötti távolság és irány. Az objektum elmozdulásának iránya a végső helyzet elérése előtt figyelmen kívül hagyható, mert csak a kezdő és a végpont közötti távolságot veszik figyelembe. Az első példában egy objektumot használunk, amely állandó sebességgel mozog egy irányban:
- Tegyük fel, hogy egy rakéta 5 percig észak felé mozog, állandó 120 méteres sebességgel. A végső pozíció kiszámításához használja az s = vt képletet, vagy használja a gyakorlati gondolkodást a rakéta által megtett távolság kiszámításához (5 perc) (120 méter/perc) = 600 méterre északra a kiindulási ponttól.
- Az állandó gyorsulással járó problémák esetén az s = vt + at paranccsal oldhatja meg őket2, vagy használja a másik részben leírt rövid módszert a válasz megtalálására.
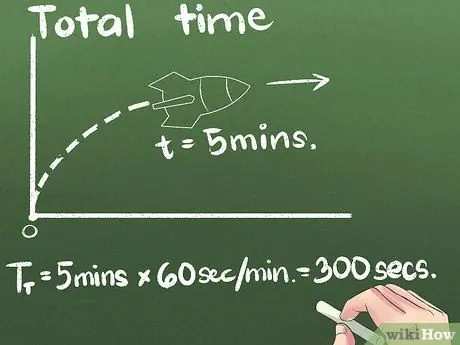
3. lépés. Keresse meg az összes eltöltött időt
Példánkban a rakéta 5 percig halad előre. Az átlagos sebességet bármely időegységben kifejezheti, de a második a nemzetközi tudományos szabványos egység. Ebben a példában megváltoztatjuk a másodpercek mértékegységét: (5 perc) x (60 másodperc/perc) = 300 másodperc.
Még tudományos problémák esetén is, ha a kérdés órát vagy nagyobb időegységet használ, először könnyebb lesz kiszámítani a sebességet, majd a végső választ méter/másodpercre konvertálni
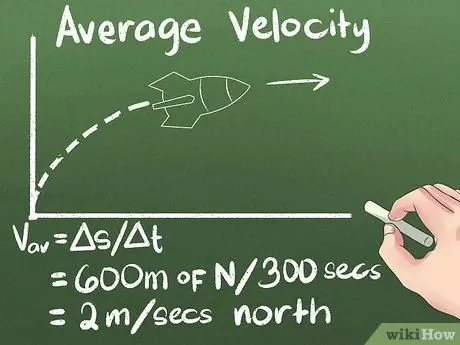
4. lépés. Számítsa ki az átlagos sebességet elmozdulásként az idő múlásával
Ha tudja, milyen messze mozog egy tárgy, és mennyi időbe telik, hogy odaérjen, akkor tudja, milyen gyorsan mozog. Tehát az általunk használt példában a rakéta átlagos sebessége (600 méter északra) / (300 másodperc) = 2 méter/másodperc északra.
- Ne felejtse el megadni az irányt (például "elülső" vagy "északi").
- A képletben vav = s/Δt. A delta szimbólum jelentése "változás", tehát az s/Δt jelentése "pozícióváltozás egy bizonyos időtartam alatt".
- Az átlagos sebesség v -ként írhatóav, vagy v -ként, fölötte vízszintes vonallal.

5. lépés Bonyolultabb problémák megoldása
Ha egy tárgy megváltoztatja az irányát vagy sebességét, ne ess zavarba. Az átlagsebességet továbbra is "csak" a teljes elmozdulás és a teljes idő alapján számítják ki. A kezdő és a végpont közötti eseményeket figyelmen kívül hagyhatja. Az alábbiakban bemutatunk néhány példát arra, hogy egy objektum ugyanazzal az elmozdulással és teljes idővel, tehát azonos átlagos sebességgel utazik:
- Anna 2 másodpercig nyugat felé halad 1 méter/s sebességgel, majd hirtelen 3 méter/másodpercre gyorsul, és 2 másodpercig folytatja a nyugati sétát. A teljes elmozdulás (1 m/s nyugat felé) (2 mp) + (3 m/s nyugat felé) (2 mp) = 8 méter nyugatra. A teljes idő 2 másodperc + 2 másodperc = 4 másodperc. Tehát az átlagos sebesség 8 méter nyugatra/ 4 másodperc = 2 méter/másodperc nyugatra.
-
Bart 3 másodpercig nyugat felé halad 5 méter/mp sebességgel, majd megfordul, és 7 másodperc/másodperc sebességgel kelet felé sétál 1 másodpercig. A keleti mozgást "negatív nyugati irányú mozgásnak" tekinthetjük, így a teljes elmozdulás = (5 méter/mp nyugat felé) (3 mp) + (-7 m/s nyugat felé) (1 mp) = 8 méter. Teljes idő = 4 másodperc. Átlagos sebesség = 8 méter nyugatra / 4 másodperc = 2 méter/másodperc nyugatra.
-
Charlotte 1 métert gyalogolt északra, majd nyugatra 8 métert, majd délre 1 métert. A teljes út teljesítése 4 másodpercig tart. Rajzolja le a diagramot egy papírra, és látni fogja, hogy a végpont 8 méterrel nyugatra van a kezdőponttól, tehát ez az érték az elmozdulás. A teljes idő 4 másodperc, tehát az átlagos sebesség 8 méter nyugatra / 4 másodperc = 2 méter/másodperc nyugatra.
2. módszer 2 -ből: A rögzített gyorsulás átlagos sebességének kiszámítása

Az átlagos sebesség kiszámítása 6. lépés 1. lépés. Tekintsük a kezdeti sebességet és az állandó gyorsulást
Tegyük fel, hogy a problémánk a következő: "Egy kerékpár jobbra halad 5 m/s sebességgel, állandó 2 m/s gyorsulással2. Ha ez a kerékpár 5 másodpercig mozog, mennyi az átlagos sebessége?"
Ha az egység "méter/másodperc2"hogy megzavarja, írja be, hogy" méter/másodperc/másodperc "vagy" méter/másodperc/másodperc ". A 2 méteres/másodperces/másodperces gyorsulás azt jelenti, hogy a sebesség másodpercenként 2 méterrel növekszik.

Az átlagos sebesség kiszámítása 7. lépés 2. lépés Gyorsítással keresse meg a végső sebességet
A gyorsulás, amelyet az a jelöléssel jelölünk, a sebesség (vagy sebesség) változásának sebessége. A sebesség állandó növekedési ütemben növekszik. Táblázatot rajzolhat a gyorsítás segítségével, hogy megtalálja a sebességet a kerékpárút során különböző időpontokban. Ezt a táblázatot létre kell hoznunk, hogy megtaláljuk a probléma végpontját (t = 5 másodperc), de létrehozunk egy hosszabb táblázatot, hogy könnyebben megértsük ezt a fogalmat:
- A kezdőponton (t = 0 másodperc) a kerékpár 5 méter/s sebességgel halad.
- 1 másodperc után (t = 1) a kerékpár 5 méter/másodperc sebességgel halad = 5 méter/másodperc + (2 méter/másodperc) sebességgel2) (1 másodperc) = 7 méter/másodperc.
- T = 2 esetén a kerékpár jobbra halad 5+ (2) (2) = 9 méter/mp sebességgel.
- T = 3 esetén a kerékpár jobbra halad 5+ (2) (3) = 11 méter/mp sebességgel.
- T = 4 esetén a kerékpár jobbra halad 5+ (2) (4) = 13 méter/mp sebességgel.
- T = 5 esetén a kerékpár jobbra halad 5+ (2) (5) = sebességgel 15 méter/másodperc.

Az átlagos sebesség kiszámítása 8. lépés Lépés 3. Ezzel a képlettel találhatja meg az átlagos sebességet
Ha és "csak", ha a gyorsulás állandó, akkor az átlagos sebesség megegyezik a végső és a kezdeti sebesség összegének átlagértékével. (vf +vén)/2. A fenti példaproblémánkhoz a kerékpár kezdeti sebessége vén 5 méter/másodperc. Miután kiszámítottuk, a végsebesség vf 15 méter/másodperc. Ezt a két értéket összeadva kapjuk (15 méter/másodperc + 5 méter/másodperc)/2 = (20 méter/másodperc)/2 = 10 méter/másodperc jobb irányba.
- Ne felejtse el feltüntetni az irányt, ebben az esetben "helyes".
- Ezt a kifejezést v0 (sebesség 0 időpontban, vagy kezdeti sebesség) és v (végsebesség).

Az átlagos sebesség kiszámítása 9. lépés 4. lépés. Értse meg intuitív módon az átlagos sebesség képletét
Az átlagos sebesség megtalálásához a sebességet bármely ponton felhasználhatjuk, és mindegyikre megtalálhatjuk az átlagot. (Ez az átlag definíciója.) Mivel ez számítást vagy végtelen időt igényel, értse meg ezt a képletet intuitívabban. Ahelyett, hogy minden alkalommal időt vesz, számítsa ki a két időpont átlagos sebességét, és nézze meg az eredményeket. Az egyik időpont az út kezdete közelében van, ahol a kerékpár lassan halad, a másik pedig a végpont közelében, ahol a kerékpár gyorsan halad.

Az átlagos sebesség kiszámítása 10. lépés 5. lépés. Tesztelje az intuitív elméletet
A fenti táblázat segítségével határozza meg a sebességet a különböző időpontokban. Néhány kritériumunknak megfelelő pár (t = 0, t = 5), (t = 1, t = 4) vagy (t = 2, t = 3). Ha akarja, tesztelheti ezt a képletet t számokkal is, nem egész számokkal.
Bármelyik pontpárt is választja, az akkori átlagos sebesség mindig ugyanaz lesz. Például ((5+15)/2), ((7+13)/2), vagy ((9+11)/2) egyenlő 10 méter/sec jobbra

Az átlagos sebesség kiszámítása 11. lépés 6. lépés. Fejezze be az intuitív magyarázatot
Ha ezt a módszert alkalmazzuk az egyes időpontok listájával, folytatjuk az utazás első felének és az utazás második felének átlagának kiszámítását. A félidő lefedése ugyanannyi időt vesz igénybe, így a sebesség megszűnik, amikor befejezzük a számlálást.
- Mivel bármelyik pár ugyanazt az eredményt adja, ezeknek a sebességeknek az átlaga is azonos lesz. Példánkban az egész sebesség "10 méter/mp jobbra" továbbra is 10 méter/sec lesz jobbra.
- Ezt az értéket bármely pár átlagának kiszámításával találhatjuk meg, például a kezdeti és a végsebességet. Példánkban ezeket a sebességeket t = 0 és t = 5 értékeknél érjük el, és a fenti képlet segítségével számíthatjuk ki: (5+15)/2 = 10 méter/sec jobbra.

Az átlagos sebesség kiszámítása 12. lépés 7. lépés. Értse meg ezt a képletet matematikailag
Ha jobban szereti a képletekként leírt bizonyításokat, akkor kezdjen egy képlettel, amely kiszámítja a megtett távolságot, állandó gyorsulást feltételezve, és onnan származtatja a képletet:
- s = vént + at2. (Technikailag s és t, vagy helyzetváltozás és időbeli változás, de akkor is megértenénk, ha s és t írnánk.)
- Átlagos sebesség vav s/t, ezért írja be a képletet s/t formában.
- vav = s/t = vén + at
- A gyorsulás x idő egyenlő a teljes sebesség változásával, vagy vf - vén. Tehát helyettesíthetjük az "at" -t a képletben, és kapjuk:
- vav = vén + (vf - vén).
- Egyszerűsítse: vav = vén + vf - vén = vén + vf = (vf +vén)/2.
Tippek
- A sebesség különbözik a sebességtől, mert a sebesség vektoros mennyiség, míg a sebesség skaláris mennyiség. A vektoros mennyiségek irányt és nagyságot tartalmaznak, míg a skaláris mennyiségek csak nagyságrendet.
- Ha az objektum egy dimenzióban mozog, például balról jobbra, akkor pozitív számot használhat az egyik irány (például jobb), és negatív számot egy másik irány (bal) ábrázolására. Írja ezt a jelölést az oldal tetejére, hogy világos legyen a munkáját olvasó emberek számára.






