- Szerző Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:13.
- Utoljára módosítva 2025-01-23 12:19.
Az elmozdulás a fizikában az objektum helyzetének megváltozását jelenti. Amikor kiszámítja az elmozdulást, kiszámítja, hogy az objektum milyen messze van a kezdeti és a végső helye alapján. Az elmozdulás kiszámításához használt képlet a feladatnak adott változótól függ. Kövesse ezeket a lépéseket az elmozdulás kiszámításához.
Lépés
1. rész az 5 -ből: Az eredő elmozdulás kiszámítása

1. lépés. Használja a kapott elmozdulási képletet, ha a távolság mértékegységét használja a kezdő és a végpont jelzésére
Bár a távolság eltér az elmozdulástól, az ebből eredő elmozdulási probléma azt vizsgálja, hogy hány kilométert vagy métert tett meg az objektum. Ezzel a mértékegységgel kiszámíthatja az elmozdulást és azt, hogy az objektum elhelyezkedése milyen messze tér el a kiindulási ponttól.
- A kapott elmozdulási képletet így írjuk fel: S = x²+y². S az elmozdulás. X a tárgy első mozgási iránya, Y pedig a tárgy második mozgási iránya. Ha az objektum csak egy irányban mozog, akkor Y = 0.
- Egy objektum legfeljebb két irányban mozoghat, mert az északi/déli vagy kelet/nyugati tengely mentén történő mozgás semleges mozgásnak minősül.

2. lépés: Csatlakoztassa a pontokat a mozgás sorrendjében, és címkézze őket A-tól Z-ig
Vonalzóval húzzon egyenes vonalat pontról pontra.
- Emellett ne felejtse el a kezdőpontot a végponttal egyenes vonallal összekapcsolni. Ezt az elmozdulást fogjuk kiszámítani.
- Például, ha egy objektum 300 m -re keletre és északra 400 m -re mozog, akkor derékszögű háromszöget alkot. AB lesz a háromszög első szára, BC pedig a második. AC lesz a háromszög hipotenúza, nagysága pedig az objektum elmozdulása. Ebben a példában a két irány kelet és észak.

3. lépés. Adja meg az x² és y² értékeket
Most, hogy ismeri az objektum két mozgási irányát, írja be az értékeket a megfelelő változókba.
Például x = 300 és y = 400. A képletnek így kell kinéznie: S = 300² + 400²
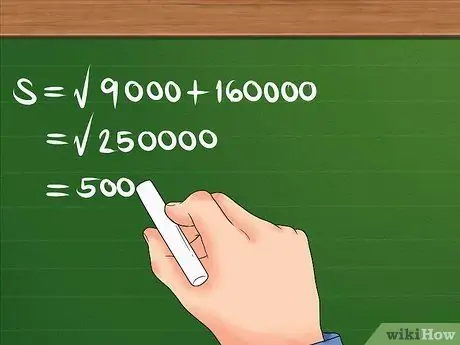
4. lépés. Számítsa ki a képletet a műveletek sorrendje alapján
Először tegye a 300 és a 400 négyzeteket, majd adja össze őket, és keresse meg az összeg négyzetgyökét.
Például: S = 90000 + 160000. S = 250000. S = 500. Most már tudja, hogy az elmozdulás 500 m
2. rész az 5 -ből: Amikor a sebesség és az idő ismert

1. lépés. Használja ezt a képletet, ha a probléma megmondja az objektum sebességét és az időt
Néhány matematikai feladat nem fogja megmondani, hogy milyen messze vagy milyen gyorsan mozog egy tárgy. Az idő és a sebesség segítségével kiszámíthatja az elmozdulást.
-
Ebben az esetben a képlet a következő lesz: S = 1/2 (u + v) t.
U = az objektum kezdeti sebessége, vagy az, hogy az objektum milyen gyorsan kezd elmozdulni egy bizonyos irányba. V = az objektum végsebessége, vagy az, hogy milyen gyorsan halad az objektum a végső helye felé. T = az az idő, amíg az objektum eléri a végső helyét.
- Példa: Egy autó 45 másodpercig megy le az úton (szükséges idő). Az autó nyugatra fordul 20 m/s sebességgel (kezdeti sebesség), és az út végén sebessége 23 m/s (végsebesség). Számítsa ki az elmozdulást ezen tényezők alapján.

2. lépés. Adja meg a kívánt sebességet és időt a megfelelő változókba
Most, hogy tudja, milyen messze halad az autó, milyen gyorsan halad az elején és a végén, megtalálhatja a kezdő hely és a végső hely közötti távolságot.
A képletének így kell kinéznie: S = 1/2 (20 + 23) 45

Lépés 3. Számítsa ki a képletet, miután az értékeket a megfelelő helyre tette
Ne felejtse el követni a műveletek sorrendjét, különben az elmozdulások nagyon eltérő értékeket eredményeznek.
- Ennél a képletnél nem számít, ha véletlenül felcseréli a kezdő és a végsebességet. Mivel először összeadja ezeket a számokat, nem számít, hogy hol vannak zárójelben. Más képletek esetében azonban a kezdeti és a végsebesség felcserélése eltérő elmozdulási értékeket eredményez.
- A képletének így kell kinéznie: S = 1/2 (43) 45. Először ossza el a 43 -at 2 -vel, aminek eredménye 21, 5. Ezután szorozza meg a 21 -et, 5 -öt 45 -tel, így az eredmény 967,5 méter. 967, 5 az elmozdulás nagysága, vagy az, hogy az autó milyen messze mozdult el a kiindulási ponttól.
3. rész az 5 -ből: Amikor a kezdeti sebesség, gyorsulás és idő ismert
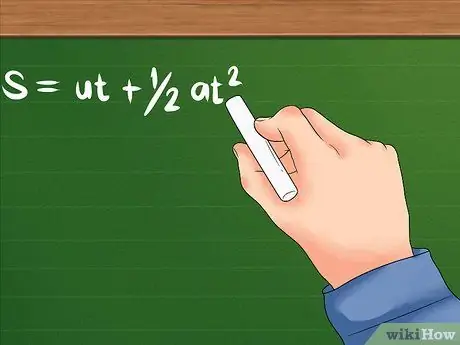
1. lépés Használja a módosított képletet, ha a gyorsulás ismert a kezdeti sebesség és idő mellett
Néhány kérdés csak azt fogja mondani, hogy az objektum milyen gyorsan mozog az elején, milyen gyorsan kezd gyorsulni, és milyen messze mozog. Szüksége lesz a következő képletre.
- A probléma képlete a következő: S = ut + 1/2 at². U továbbra is a kezdeti sebességet jelzi; a a tárgy gyorsulása, vagy milyen gyorsan kezd változni a sebessége. T jelentheti azt az időt, amelyre szükség van, vagy egy bizonyos ideig, amíg egy objektum felgyorsul. Mindkettő olyan időegységeket fog használni, mint a másodperc, az óra és mások.
- Tegyük fel, hogy egy 25 m/s sebességgel haladó autó (kezdeti sebesség) 3 m/s2 (gyorsulás) sebességgel gyorsulni kezd 4 másodpercig (idő). Mekkora az autó térfogata 4 másodperc után?

2. lépés. Írja be az értékeket a képletbe
Az előző képlettől eltérően itt csak a kezdeti sebesség szerepel, ezért ügyeljen a helyes adatok megadására.
A fenti mintaadatok alapján a képlet így nézne ki: S = 25 (4) + 1/2 (3) 4². Segítségével zárójeleket adhat hozzá a gyorsulás nagyságához és idejéhez, hogy segítsen elkülöníteni a számokat
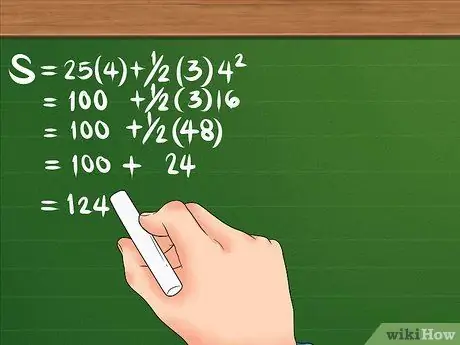
3. lépés. Számítsa ki az elmozdulást a műveletek helyes sorrendjében
A műveletek sorrendjének emlékezésének gyors módja a Kur ir Kua ci Kadang Ba wa Juragan Turtles szamárhíd. Ez a helyes sorrendet képviseli: zárójelek, négyzetek, szorzás, osztás, összeadás és kivonás.
Nézzük újra a képletet: S = 25 (4) + 1/2 (3) 4². Először a 4. négyzetet, az eredmény 16. Ezután szorozza meg a 16 -at 3 -mal, így 48; majd szorozzuk meg a 25 -öt 4 -gyel is, hogy 100 -at kapjunk. Oszd meg a 48 -at 2 -vel, hogy legyen 24. Az egyenleted így néz ki: S = 100 + 24. Ha összeadod a kettőt, az elmozdulás 124 méter
4. rész az 5 -ből: Szögeltolás kiszámítása

1. lépés Keresse meg a szögbeli elmozdulást, amikor az objektum körpályán mozog
Bár az elmozdulást továbbra is egyenes vonallal számítja ki, meg kell találnia a különbséget az objektum kezdő és befejező helye között, amint körkörös úton halad.
- Képzeljünk el egy lányt, aki körhintán ül. Miközben forog a körhintával, körkörös úton fog haladni. A szögeltolódás megpróbálja megtalálni a legrövidebb távolságot a kezdeti és a végső hely között, amikor az objektum nem egyenes vonalban mozog.
- A szögeltolás képlete a következő: = S/r, ahol S a lineáris elmozdulás, r a sugár és a szögeltolódás. A lineáris elmozdulás az, hogy az objektum milyen messze mozog egy ív mentén. A sugár az objektum távolsága a kör középpontjától. A szögeltolódás az az érték, amelyet meg akarunk találni.

2. lépés Csatlakoztassa a lineáris elmozdulást és a sugarat az egyenlethez
Ne feledje, hogy a sugár a kör középpontjától való távolság; néhány probléma megmondja a kör átmérőjét, amelyet 2 -el kell osztani a sugár megtalálásához.
- Íme egy példa probléma: Egy lány körhintán lovagol. Az ülés 1 méterre van a kör közepétől (a sugár). Ha a lány 1,5 méteres ívpályán mozog (lineáris elmozdulás), mi a szögbeli elmozdulása?
- Az egyenlete így fog kinézni: = 1,5/1.
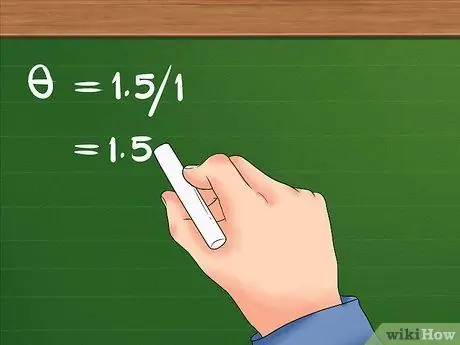
3. lépés. Oszd meg a lineáris elmozdulást a sugárral
Ez a felosztás az objektum szögbeli elmozdulását eredményezi.
- Az 1,5 -ös 1 -gyel való elosztása után az eredmény 1,5, A lány szögeltolódása 1,5 radiánok.
- Mivel a szögbeli elmozdulás azt méri, hogy egy tárgy mennyiben forog a kezdeti helyzetéből, szögként kell mérni, nem pedig távolságként. A radián a szögek mérésére használt egység.
5. rész az 5 -ből: A migráció megértése
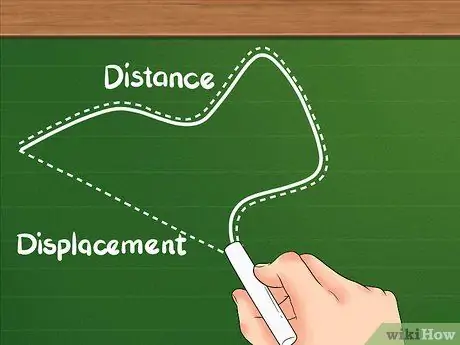
1. lépés. Tudja, hogy a távolságnak más a meghatározása, mint az elmozdulásnak
A távolság megmutatja, hogy milyen messze van az objektum által megtett teljes távolság.
- A távolságot gyakran skaláris mennyiségnek nevezik. A távolság megmutatja az objektum által megtett távolságot a tárgy irányától függetlenül.
- Például, ha 2 lépést tesz keletre, 2 lépést délre, 2 lépést nyugatra, majd 2 lépést északra, akkor visszatér a kiindulási helyzetébe. Annak ellenére, hogy átélted a teljes összeget távolság 10 lépésnyire, csak mozog 0 lépésre van, mert a végső tartózkodási helye megegyezik a kiindulási hellyel (az útvonal egy dobozra hasonlít).

2. lépés. Értsd meg, hogy az elmozdulás a két hely közötti különbség
Az elmozdulás nem a mozgás teljes összege, mint a távolság; A váltás a kezdő és a befejező hely közötti területre összpontosít.
- Az elmozdulást vektormennyiségnek nevezzük, és az objektum helyzetének változását mutatja, figyelembe véve a tárgy mozgási irányát.
- Például 5 lépést tesz kelet felé. Ha 5 lépéssel visszamegy nyugatra, akkor az eredeti helyével ellentétes irányba fog haladni. Annak ellenére, hogy megtett 10 lépést, helyzete nem változott; az elmozdulás 0 lépés.

3. lépés. Ne feledje a szavakat előre és hátra, amikor megpróbálja elképzelni az elmozdulást
Az ellenkező irányba történő mozgás kiküszöböli a tárgy elmozdulását.
Képzeljünk el egy fociedzőt oda -vissza a pálya szélén. Ahogy a játékosoknak kiabált, többször balról jobbra váltott. Ha figyeli, ahogy balról jobbra halad, megfigyelheti a teljes megtett távolságot. Tegyük fel azonban, hogy az edző megáll, hogy a pálya szélén beszéljen a hátvéddel. Ha a költözés előtt más helyen tartózkodik, mint a kezdeti helye, akkor megfigyelheti az edző mozgását

4. Lépés. Tudja, hogy az elmozdulást egyenes, és nem körút segítségével mérik
Az elmozdulás megtalálásához meg kell találnia a legrövidebb és leghatékonyabb módszert a két pont közötti különbség kiszámításához.
- Körkörös út vezet a kiindulási helyről a végső helyre, de nem ez a legrövidebb út. A vizualizálás érdekében képzelje el, hogy egyenes vonalban jár, és egy oszlopra bukkan. Ezt az oszlopot nem tudod áttörni, ezért megkerülöd. Annak ellenére, hogy a végső pozíciója ugyanaz, mintha áttörte az oszlopot, további lépésekre lesz szüksége a cél eléréséhez.
- Bár az elmozdulás egyenes utat jelent, tudd, hogy meg tudod mérni az objektum elmozdulását jelenleg körúton haladni. Ezt az elmozdulást szögeltolódásnak nevezik, és kiszámítható a kezdeti helytől a végső helyre vezető legrövidebb út megkeresésével.

5. lépés. Tudja, hogy az elmozdulás negatív is lehet, ellentétben a távolsággal
Ha a végső helyét úgy éri el, hogy a kezdeti irányával ellentétes irányban mozog, akkor az elmozdulás negatív.
- Például 5 lépést sétálunk keletre, majd 3 lépést nyugatra. Annak ellenére, hogy számításokkal 2 lépést tesz ki a kiindulási helytől, elmozdulása -2, mert az ellenkező irányba halad. A távolság mindig pozitív lesz, mert nem tud visszafelé számolni lépésekben, kilométerekben stb.
- A negatív elmozdulás nem jelenti azt, hogy az elmozdulás csökken. A negatív csak azt jelenti, hogy az irány ellentétes.

6. Lépés. Vegye észre, hogy néha a távolság és az elmozdulás ugyanaz lehet
Ha 25 lépést egyenesen sétál, és megáll, a megtett távolság megegyezik az eredeti helyétől való elmozdulással.
- Ez csak akkor érvényes, ha egy helyről egyenes vonalban mozog a kiindulási helyről. Például San Franciscóban él, Kaliforniában, és új állást kap Las Vegasban, Nevadában. El kell költöznie Las Vegasba, hogy közel legyen a munkahelyéhez. Ha felszáll egy repülőgépre, amely repül egyenes San Franciscóból Las Vegasba ugyanazt a távolságot és elmozdulást fogja megtenni x.
- Ha azonban San Franciscóból Las Vegasba utazik, akkor x távolságot fog megtenni, de y távolságot. Mivel az autóvezetésnek általában változó irányai vannak (ettől az úttól keletre, az úttól nyugatra), hosszabb távolságokat kell megtennie, mint a két város közötti legrövidebb távolság.






