3 módszer a gőznyomás kiszámítására

2024 Szerző: Jason Gerald | [email protected]. Utoljára módosítva: 2024-02-01 14:13

Hagytál már egy üveg vizet néhány órán át a forró napon, és enyhe "sziszegő" hangot hallottál, amikor kinyitod? Ennek oka a gőznyomásnak nevezett elv. A kémiában a gőznyomás az a nyomás, amelyet a zárt tartály falai okoznak, amikor a benne lévő kémiai anyag elpárolog (gázgá alakul). A gőznyomás meghatározásához adott hőmérsékleten használja a Clausius-Clapeyron egyenletet: ln (P1/P2) = (ΔH_gőz/R) ((1/T2) - (1/T1)).

Lépés

1. módszer a 3-ból: A Clausius-Clapeyron egyenlet használata

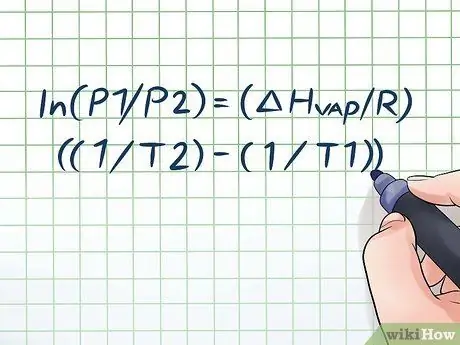
1. lépés Írja le a Clausius-Clapeyron egyenletet

A gőznyomásnak a gőznyomás időbeli változásával történő kiszámításához használt képletet Clausius – Clapeyron egyenletnek nevezik (Rudolf Clausius és Benoît Paul mile Clapeyron fizikusokról nevezték el.) Ez alapvetően az a képlet, amelyre a legtöbb típusú probléma megoldásához szüksége lesz A gőznyomással kapcsolatos kérdések gyakran megtalálhatók a fizika és a kémia órán. A képlet a következő: ln (P1/P2) = (ΔH_gőz/R) ((1/T2) - (1/T1)). Ebben a képletben a változók a következők:

H_gőz:

A folyadék párolgásának entalpiája. Ez az entalpia általában megtalálható a kémia tankönyv hátulján található táblázatban.
R:

A valós/univerzális gázállandó, vagy 8,314 J/(K × Mol).
Q1:

Az a hőmérséklet, amelyen a gőznyomás ismert (vagy kezdeti hőmérséklet).
T2:

Az a hőmérséklet, amelynél a gőznyomás ismeretlen/megtalálható (vagy a végső hőmérséklet).
P1 és P2:

Gőznyomás T1 és T2 hőmérsékleten.

2. lépés. Írja be az ismert változókat

A Clausius-Clapeyron egyenlet bonyolultnak tűnik, mert sok különböző változót tartalmaz, de valójában nem olyan nehéz, ha megfelelő információval rendelkezik. A legtöbb alapvető gőznyomás -probléma két hőmérsékleti értéket és egy nyomásértéket, vagy két nyomásértéket és egy hőmérsékletértéket fog felsorolni - ha ezt kitalálja, ennek az egyenletnek a megoldása nagyon egyszerű.

Tegyük fel például, hogy azt mondják nekünk, hogy van egy folyadékkal teli edényünk 295 K -on, amelynek gőznyomása 1 atmoszféra (atm). Kérdésünk a következő: Mekkora a gőznyomás 393 K -on? Két hőmérséklet- és egy nyomásértékünk van, így a többi nyomásértéket a Clausius-Clapeyron-egyenlet segítségével találhatjuk meg. Ha bekapcsoljuk a változóinkat, azt kapjuk ln (1/P2) = (ΔH_gőz/R) ((1/393) - (1/295)).
Vegye figyelembe, hogy a Clausius-Clapeyron egyenlethez mindig a hőmérséklet értékét kell használnia Kelvin. Bármilyen nyomásértéket használhat, amíg a P1 és P2 értékei megegyeznek.

3. lépés. Adja meg az állandókat

A Clausius-Clapeyron egyenletnek két állandója van: R és H_gőz. R mindig 8,314 J/(K × Mol). Azonban H._gőz (párolgási entalpia) attól az anyagtól függ, amelynek gőznyomását keresi. Amint fentebb említettük, általában megtalálhatja a H értékeit_gőz különböző anyagokhoz a kémia vagy fizika tankönyv hátulján, vagy online (például itt.)

Példánkban tegyük fel, hogy a folyadékunk az tiszta víz.

Ha a táblázatban megnézzük a H értékeit_gőz, azt találjuk, hogy H_gőz tiszta víz körülbelül 40,65 KJ/mol. Mivel a H értékünk joule -ban, és nem kilojoule -ban van, át tudjuk alakítani 40 650 J/mol.
Ha bekapcsoljuk az állandóinkat, megkapjuk ln (1/P2) = (40 650/8, 314) ((1/393) - (1/295)).

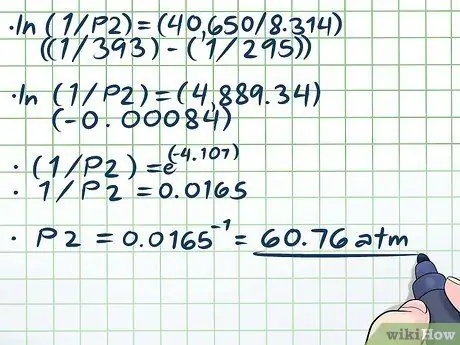
4. lépés. Oldja meg az egyenletet

Miután az összes változót beillesztette az egyenletbe, kivéve a keresettet, folytassa az egyenlet megoldását a közönséges algebra szabályai szerint.

Az egyenlet megoldásának egyetlen nehéz része (ln (1/P2) = (40 650/8, 314) ((1/393) - (1/295))) feloldja a természetes naplót (ln). A természetes napló eltávolításához használja az egyenlet mindkét oldalát kitevőként az e matematikai állandóhoz. Más szavakkal, ln (x) = 2 → e^{ln (x)} = e² → x = e².
Most oldjuk meg egyenletünket:
ln (1/P2) = (40 650/8, 314) ((1/393) - (1/295))
ln (1/P2) = (4889, 34) (-0, 00084)
(1/P2) = e^{(-4, 107)}
1/P2 = 0,0165
P2 = 0,0165^-1 = 60, 76 atm.

Ennek van értelme - zárt edényben a hőmérséklet közel 100 fokosra (majdnem 20 fokra a forráspont fölé) emelése sok gőzt termel, ami gyorsan növeli a nyomást.

2. módszer a 3 -ból: Gőznyomás meghatározása oldott oldattal

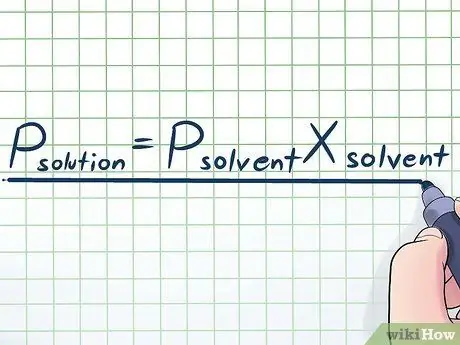
1. lépés Írja le Raoult törvényét

A való életben ritkán dolgozunk tiszta folyadékkal - általában olyan folyadékkal dolgozunk, amely több különböző anyag keveréke. A leggyakrabban használt keverékek némelyike úgy készül, hogy bizonyos oldott anyagnak nevezett vegyi anyagot kis mennyiségben feloldunk oldószerként. Ezekben az esetekben hasznos megismerni a Raoult-törvény (François-Marie Raoult fizikus nevét viselő) egyenletet, amely így van írva: P_oldott= P_oldószerx_oldószer. Ebben a képletben a változók jelentik;

P_oldott:

A teljes oldat gőznyomása (az összes elem együtt)
P_oldószer:

Oldószer gőznyomás
x_oldószer:

Az oldószer mólrésze
Ne aggódjon, ha nem ismer olyan kifejezéseket, mint a vakond tört - a következő néhány lépésben elmagyarázzuk azokat.

2. lépés. Határozza meg az oldószert és oldja fel az oldatban

Mielőtt kiszámíthatná a vegyes folyadék gőznyomását, meg kell határoznia a felhasznált anyagokat. Emlékeztetőül: oldat keletkezik, amikor egy oldott anyag oldódik oldószerben - az oldódó vegyi anyagot mindig oldott anyagnak nevezik, és az oldódást előidéző vegyi anyagot mindig oldószernek.

Dolgozzunk az ebben a szakaszban található egyszerű példák segítségével, hogy szemléltessük a tárgyalt fogalmakat. Például tegyük fel, hogy meg akarjuk találni a cukorszirup gőznyomását. Hagyományosan a cukorszirup vízben oldódó cukor (1: 1 arány), így azt is mondhatjuk a cukor az oldott anyagunk, a víz pedig az oldószerünk.
Vegye figyelembe, hogy a szacharóz (asztali cukor) kémiai képlete C₁₂H₂₂O₁₁. Ez a kémiai képlet nagyon fontos lesz.

3. lépés. Keresse meg az oldat hőmérsékletét

Amint azt a fenti Clausius Clapeyron részben láttuk, a folyadék hőmérséklete befolyásolja a gőznyomását. Általában minél magasabb a hőmérséklet, annál nagyobb a gőznyomás - a hőmérséklet emelkedésével a folyadék nagyobb része elpárolog és gőzt képez, növelve a tartályban lévő nyomást.

Példánkban tegyük fel, hogy a cukorszirup hőmérséklete ezen a ponton van 298 K (kb 25 C).

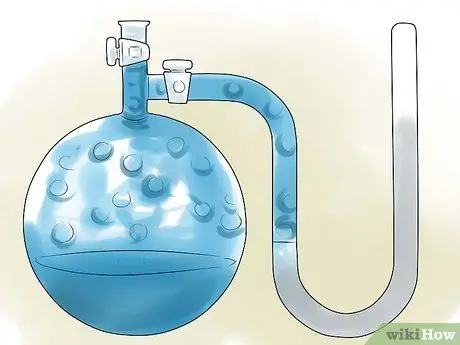
4. lépés Keresse meg az oldószer gőznyomását

A kémiai referenciaanyagok általában számos általánosan használt anyag és vegyület esetében rendelkeznek gőznyomás értékekkel, de ezek a nyomásértékek általában csak akkor érvényesek, ha az anyag hőmérséklete 25 C/298 K vagy forráspontja. Ha az oldat ezen hőmérsékletek egyikével rendelkezik, használhat referenciaértéket, de ha nem, akkor meg kell találnia a gőznyomást ezen a hőmérsékleten.

A Clausius -Clapeyron segíthet - használjon referencia gőznyomást és 298 K (25 C) értéket P1 és T1 esetén.
Példánkban keverékünk hőmérséklete 25 C, így könnyen használhatjuk az egyszerű referencia táblázatunkat. Tudjuk, hogy 25 C -on a víz gőznyomása 23,8 mm HG

5. lépés Keresse meg az oldószer móltörtét

Az utolsó dolog, amit meg kell tennünk, mielőtt ezt meg tudjuk oldani, hogy megtaláljuk az oldószerünk móltöredékét. A mólfrakció megtalálása egyszerű: csak alakítsa át vegyületeit mollra, majd keresse meg az egyes vegyületek százalékos arányát az anyag összes móljában. Más szóval, az egyes vegyületek móltörtje egyenlő (vegyület móljai)/(az anyagi mólok teljes száma).

Tegyük fel, hogy a cukorszirup használatára vonatkozó receptünk 1 liter (L) víz és 1 liter szacharóz (cukor).

Ebben az esetben meg kell találnunk az egyes vegyületek móljainak számát. Ehhez meg fogjuk találni az egyes vegyületek tömegét, majd az anyag moláris tömegével alakítjuk át molokká.
Tömeg (1 liter víz): 1000 gramm (g)
Tömeg (1 l nyerscukor): kb. 1056, 8 g
Mól (víz): 1000 gramm × 1 mol/18,015 g = 55,51 mol
Mólok (szacharóz): 1056, 7 gramm × 1 mol/342,2965 g = 3,08 mol (vegye figyelembe, hogy a szacharóz moláris tömegét a kémiai képletéből találja, C₁₂H₂₂O₁₁.)
Összes mol: 55,51 + 3,08 = 58,59 mol
A víz mólrésze: 55, 51/58, 59 = 0, 947

6. lépés. Befejezés

Végül megvan minden, amire szükségünk van Raoult -törvény egyenletének megoldásához. Ez a rész nagyon egyszerű: csak adja meg a változók értékeit az egyszerűsített Raoult -törvény egyenletben a szakasz elején (P_oldott = P_oldószerx_oldószer).

Értékeink megadásával a következőket kapjuk:
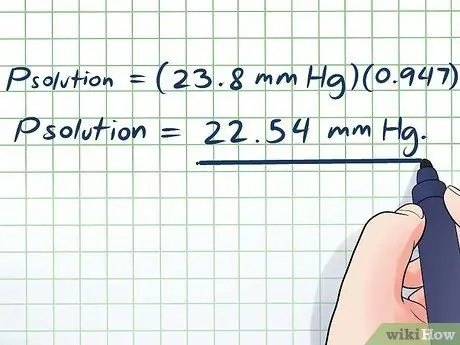
P_megoldás = (23,8 Hgmm) (0, 947)
P_megoldás = 22,54 Hgmm.

Az eredménynek van értelme - molban kifejezve nagyon kevés cukor van feloldva sok vízben (bár a valóságban mindkét összetevő térfogata azonos), így a gőznyomás csak kismértékben csökken.

3. módszer a 3 -ból: Gőznyomás megállapítása speciális esetekben

1. lépés: Legyen óvatos a normál hőmérséklet- és nyomásviszonyokkal

A tudósok gyakran használnak hőmérséklet- és nyomásértékeket egy könnyen használható „szabványként”. Ezeket az értékeket standard hőmérsékletnek és nyomásnak (STP) nevezik. A gőznyomás problémák gyakran az STP körülményeire vonatkoznak, ezért fontos megjegyezni ezeket az értékeket. Az STP értékek a következők:

Hőfok: 273, 15 K. / 0 C / 32 F
Nyomás: 760 Hgmm / 1 atm / 101, 325 kilopascal

2. lépés: A Clausius-Clapeyron egyenlet átrendezésével keresse meg a többi változót

Rész példájában láttuk, hogy a Clausius – Clapeyron egyenlet nagyon hasznos a tiszta anyagok gőznyomásának megállapításához. Azonban nem minden kérdés fogja megkérni, hogy keressen P1 vagy P2 - sokan azt fogják kérni, hogy keresse meg a hőmérséklet értékét, vagy néha a H értékét is._gőz. Szerencsére ezekben az esetekben a helyes válasz megszerzése egyszerűen az egyenlet átrendezése, hogy a megoldani kívánt változók az egyenlőjel egyik oldalán elkülönüljenek.

Tegyük fel például, hogy ismeretlen folyadékunk van, amelynek gőznyomása 25 torr 273 K -nál és 150 torr 325 K -nál, és meg akarjuk találni ennek a folyadéknak a párolgási entalpiáját (ΔH_gőz). Ezt így tudjuk megoldani:
ln (P1/P2) = (ΔH_gőz/R) ((1/T2) - (1/T1))
(ln (P1/P2))/((1/T2) - (1/T1)) = (ΔH_gőz/R)
R × (ln (P1/P2))/((1/T2) - (1/T1)) = H_gőz Most beírjuk értékeinket:
8, 314 J/(K × Mol) × (-1, 79)/(-0, 00059) = H_gőz
8, 314 J/(K × Mol) × 3033, 90 = H_gőz = 25 223, 83 J/mol

3. lépés Számítsa ki az oldott anyag gőznyomását, amikor az anyag gőzt termel

A fenti Raoult -törvény példánkban az oldott anyagunk, a cukor normál hőmérsékleten nem gyakorol önálló nyomást (gondoljunk csak - mikor látta utoljára, hogy egy tál cukor elpárolog a felső szekrényben?) elpárolog, ez befolyásolja a gőznyomását. Ezt a Raoult -törvény egyenletének egy módosított változatával számoljuk el: P_megoldás = (P._összetettx_összetett) A szigma (Σ) szimbólum azt jelenti, hogy csak össze kell adnunk a különböző vegyületek összes gőznyomását, hogy megkapjuk a választ.

Tegyük fel például, hogy van egy megoldásunk, amely két vegyszerből áll: benzolból és toluolból. Az oldat teljes térfogata 12 ml (ml); 60 ml benzol és 60 ml toluol. Az oldat hőmérséklete 25 ° C, és ezen vegyszerek gőznyomása 25 ° C -on 95,1 Hgmm benzol és 28,4 Hgmm toluol esetén. Ezekkel az értékekkel keresse meg az oldat gőznyomását. Ezt a következőképpen tehetjük meg, a két vegyi anyag standard sűrűsége, moláris tömege és gőznyomásának értékei alapján:
Tömeg (benzol): 60 ml = 0,060 liter és 876,50 kg/1000 l = 0,053 kg = 53 g
Tömeg (toluol): 0,060 L & alkalommal 866, 90 kg/1000 L = 0,052 kg = 52 g
Mol (benzol): 53 g × 1 mol/78, 11 g = 0,679 mol
Mól (toluol): 52 g × 1 mol/92, 14 g = 0,564 mol
Mólok összesen: 0,679 + 0,564 = 1,243
Mólfrakció (benzol): 0,679/1, 243 = 0,546
Mólfrakció (toluol): 0,564/1, 243 = 0,454
Megoldás: P._megoldás = P_benzolx_benzol + P._toluolx_toluol
P_megoldás = (95,1 mm Hg) (0, 546) + (28,4 mm Hg) (0, 454)
P_megoldás = 51,92 Hgmm + 12,89 Hgmm = 64, 81 Hgmm

Tippek

A fenti Clausius Clapeyron -egyenlet használatához a hőmérsékletet Kelvinben (K -ban írva) kell mérni. Ha Celsius -fokban van a hőmérséklete, akkor azt a következő képlet segítségével kell átalakítani: T_k = 273 + T._c
A fenti módszerek használhatók, mivel az energia pontosan arányos az alkalmazott hőmennyiséggel. A folyadék hőmérséklete az egyetlen környezeti tényező, amely befolyásolja a gőznyomást.