- Szerző Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:17.
- Utoljára módosítva 2025-01-23 12:20.
A tizedes (alap tízes) számrendszer tíz lehetséges értékkel rendelkezik (0, 1, 2, 3, 4, 5, 6, 7, 8 vagy 9) minden számpozícióhoz. Ezzel szemben a bináris (kettes alap) számrendszer csak két lehetséges értéket tartalmaz, mindegyik számpozíciónál 0 -t és 1 -et. Mivel a bináris számrendszer az elektronikus számítógépek belső nyelve, a komoly számítógépes programozók tudják, hogyan kell átalakítani a tizedes számrendszerből bináris számrendszerbe. Kövesse ezeket az egyszerű lépéseket, és azt is, hogyan lehet elsajátítani ezt a konverziót.
Lépés
1. módszer 2 -ből: Rövid osztás kettővel maradékkal

1. lépés. Határozza meg a problémát
Ebben a példában konvertáljuk a 156 tizedes számot10 legyen bináris szám. Írja fel a tizedes számot osztandó számként a fordított osztás szimbólumba. Írja be a rendeltetési számrendszer alapját (ebben a példában „2” a binárishoz), mint az osztási szimbólum görbén kívüli osztóját.
- Ezt a módszert sokkal könnyebb megérteni, ha papírra rajzolják, és sokkal könnyebb a kezdőknek, mert csak kettővel oszt.
- Az átváltás előtti és utáni félreértések elkerülése érdekében írja alá minden számhoz alszámként a számított számrendszer alapszámát (a kisbetűket normál betűkkel megkülönböztető jelként). Ebben a példában a tizedes szám 10 -es, a bináris szám pedig 2 -es lesz.

2. lépés Végezze el az osztást
Írja az egész választ (hányadost) a hosszú osztás szimbólum alá, a maradékot (0 vagy 1) pedig az osztott számtól jobbra.
Mivel osztunk kettővel, amikor a felosztandó szám páros szám, akkor a maradék 0, és ha az osztott szám páratlan szám, akkor a maradék 1

Lépés 3. Folytassa az osztást, amíg el nem éri a nullát
Folytassa a lefelé haladást, minden új hányadost osszon el kettővel, a maradékot pedig írja fel minden osztott szám jobbra. Állítsa le, ha a hányados nulla.

4. lépés. Írja le az új bináris számot
A legalacsonyabb fennmaradó számtól kezdve olvassa el a maradék sorrendjét növekvő sorrendben a tetejére. Ebben a példában az 10011100 eredményt kell kapnia. Ez a 156 -os tizedes szám bináris megfelelője, vagy ha numerikus alaindexével írjuk: 15610 = 100111002.
Ez a módszer módosítható úgy, hogy a tizedes bázisból bármilyen számbázisra konvertálható. Az osztó 2, mert a célszámrendszer alapja a 2 bázis (bináris). Ha a rendeltetési számrendszer alapja egy másik bázis, cserélje le a 2. bázis számot ebben a módszerben a megfelelő bázisszámmal. Például, ha a célállomás a 9. bázis, cserélje le a 2. bázis számát 9. A végeredmény közvetlenül a célállomás számának formájában lesz
2. módszer 2 -ből: Kettő ereje és kivonása

1. lépés. Kezdje egy táblázat létrehozásával
Írja le a két alapszám erejét a "2. táblázat alapja" jobbról balra. Kezdés 2 -kor0, írja be „1” -ként. Növelje a rangot 1 -gyel minden rang esetén. Töltse ki a táblázatot mindaddig, amíg meg nem kap egy számot, amely a legközelebb van a számított tizedes számrendszer számához. Ebben a példában konvertáljuk a 156 tizedes számot10 legyen bináris szám.

2. lépés. Keresse meg azt a számot, amely a 2. alapszám legnagyobb erejével rendelkezik
A táblázatból válassza ki a legnagyobb számot, amely egyenlő vagy kevesebb, mint a konvertálandó szám. A 128 -as szám a 2 -es alapszám legnagyobb teljesítménye, és kisebb is, mint 156, ezért írjon egy "1" számot a táblázat ezen mezője alá, ahol a táblázat legnagyobb száma a bal oldalon található (lásd a táblázatot) a fenti képen). Ezután vonja le a 128 -at az eredeti számból, és kap: 156 - 128 = 28.
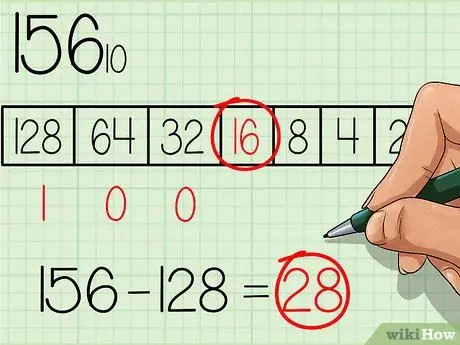
Lépés 3. Folytassa a táblázat következő kisebb teljesítményével
Az új szám (28) használatával folytassa a táblázatot balról jobbra, miközben ellenőrzi, hogy a számok megegyeznek -e az új számmal vagy kisebbek. A 64 -es szám nem kevesebb 28 -nál, ezért írja be a „0” számot a 64. számmezőbe. Folytassa, amíg 28 -as vagy annál kisebb számot nem talál.
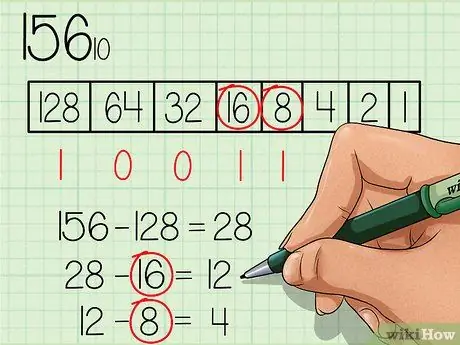
Lépés 4. Vonjon le minden olyan számot, amely egyenlő vagy kisebb, mint az új szám, és jelölje be az „1” számot a megfelelő szám mezője alatt
A 16 -os szám kevesebb, mint 28, ezért írja be az "1" számot a 16 -os számmező alá, és vonja le a 16 -ot a 28 -ból, így kap egy új 12 -es számot. A 8 -as szám kevesebb, mint 12, ezért írja be az "1" számot írja be a 8 -as számmezőt, és vonja le a 8 -at 12 -ből, hogy megkapja az új 4 -es számot.

5. lépés. Folytassa, amíg el nem éri a táblázat végét
Ne felejtsen el minden egyes mezőben „1” -et jelölni az új számmal megegyező vagy annál kisebb számoknál, és „0” -ot minden mező alatt azoknál a számoknál, amelyek még mindig nagyobbak, mint az új szám.
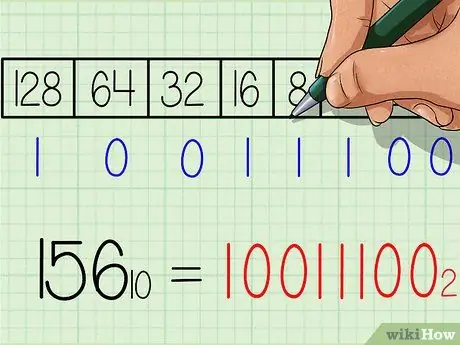
6. lépés. Írja le a bináris számra adott választ
A szám balról jobbra pontosan ugyanaz lesz, mint a táblázat alján található „1” és „0” számsor. A 10011100 eredményt kell kapnia. Ez a 156 -os tizedes szám bináris megfelelője. Vagy ha aláírással írjuk: 15610 = 100111002.
Ennek a módszernek a megismétlése segít emlékezni a második alap erejére, így kihagyhatja az 1. lépést
Tippek
- Az operációs rendszerbe épített Számológép program képes elvégezni ezt a konverziót az Ön számára, de programozóként a legjobb, ha jól ismeri a konverziók működését. A Számológép program konverziós beállításai láthatóvá tehetők a „Nézet” menü megnyitásával és a „Programozó” kiválasztásával (Windows 7 és 8 esetén).
- Az ellenkező irányba, azaz a binárisból a tizedesszámrendszerbe való konvertálást általában könnyebb először megtanulni.
- Gyakran gyakorolja a tizedes számok binárisra konvertálását, hogy szakértőbb legyen.






