- Szerző Jason Gerald [email protected].
- Public 2024-01-19 22:12.
- Utoljára módosítva 2025-01-23 12:19.
A béta egy adott részvény volatilitása vagy kockázata a teljes tőzsde volatilitásához képest. A béta azt jelzi, hogy egy adott részvény mennyire kockázatos, és annak várható hozamának értékelésére használják. A béta az egyik alap, amelyet a részvényelemzők figyelembe vesznek, amikor részvényeket választanak portfóliójukhoz, az ár / nyereség arány, a saját tőke, az adósság / részvény arány és egyéb tényezők mellett.
Lépés
Rész 1 /4: Béta kiszámítása egyszerű egyenletek segítségével

1. lépés. Keresse meg a kockázatmentes arány szintjét
Ezt a megtérülési rátát várják el a befektetők az olyan befektetésekről, amelyek pénze nem kockázatos. Ezt az értéket általában százalékban fejezik ki.

2. lépés. Határozza meg az egyes reprezentatív indexek szintjét
Ezeket az adatokat is százalékban fejezik ki. Általában a megtérülési ráta több hónapra szól.
Ezen értékek egyike vagy mindkettő negatív lehet, ami azt jelenti, hogy a részvényben vagy a piacon (indexben) végzett befektetés az időszak során veszteséget szenvedett el a befektetéssel szemben. Ha a 2 szint közül csak az egyik negatív, a béta negatív lesz

3. lépés: Vonja le a kockázatmentes kamatlábat a részvény hozamrátájából
Ha a részvény hozama 7 százalék, a kockázatmentes pedig 2 százalék, akkor 5 százalék lesz a különbség.

4. lépés: Vonja le a kockázatmentes arányt a piaci (vagy index) megtérülési rátából
Ha a piaci ár- vagy hozamindex 8 százalék, a kockázatmentes ráta pedig ismét 2 százalék, akkor a különbség 6 százalék lesz.

Lépés 5. Oszd meg a részvény hozamráta és a kockázatmentes kamatláb közötti különbözetet a piaccal (vagy indexszel), a megtérülési ráta mínusz a kockázatmentes árfolyammal
Ez egy béta verzió, amelyet általában tizedes értékként fejeznek ki. A fenti példában a béta 5 osztva 6 -tal, vagy 0,833.
- A piac bétája, vagy az általa képviselt index 1,0, mivel a piacot önmagához hasonlítják, és a nulla szám önmagával osztva 1. Az 1 -nél kisebb béta azt jelenti, hogy a részvény kevésbé ingadozó, mint a piac az egész, míg az 1 -nél nagyobb béta azt jelenti, hogy a részvény stabilabb, mint a piac egésze. A béta érték kisebb lehet nullánál, ami azt jelenti, hogy a részvény pénzt veszít, miközben a piac egésze pénzt nyer, vagy a részvény ideiglenes pénzt nyer, és a piac egésze pénzt veszít.
- A béta keresésekor, bár ez nem kötelező, általában annak a piacnak a reprezentatív indexét kell használni, ahol a részvény kereskedik. A nemzetközileg forgalmazott részvények esetében az MSCI EAFE (amely Európát, Ausztráliát és Keletet képviseli) megfelelő reprezentatív index.
Rész 2 /4: Béta használata a megtérülési árfolyam meghatározásához

1. lépés. Keresse meg a kockázatmentes arány szintjét
Ez megegyezik a fent leírt értékkel "Béta kiszámítása részvényre". Ebben a részben ugyanazt az értéket fogjuk használni, mint a 2 százalékos példát, mint a fentiekben.

2. lépés Határozza meg a piaci megtérülési rátát vagy egy reprezentatív indexet
Ebben a példában ugyanazt a 8 százalékot fogjuk használni, mint a fentiekben.

3. lépés: Szorozzuk meg a béta értéket a piaci hozam és a kockázatmentes kamatláb különbségével
Például 1,5-ös béta-értéket fogunk használni. Ha a kockázatmentes kamatlábhoz 2 százalékot, a piaci hozamhoz pedig 8 százalékot használunk, akkor ez 8-2 vagy 6 százalék lesz. 1,5 -ös bétával megszorozva 9 százalékot kapunk.
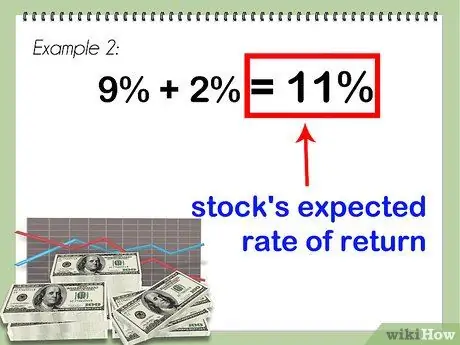
4. lépés. Adja hozzá az eredményt a kockázatmentes kamatlábhoz
11 százalékot hoz, ami a részvény várható hozama.
Minél magasabb a részvény béta értéke, annál magasabb a várható hozam. Ez a magasabb hozam azonban fokozott kockázattal párosul, ezért meg kell vizsgálni más alapvető részvényeket, mielőtt mérlegelnénk, hogy azok a befektetői portfólió részét képezik -e
3. rész a 4 -ből: Excel -diagramok használata a béta meghatározásához
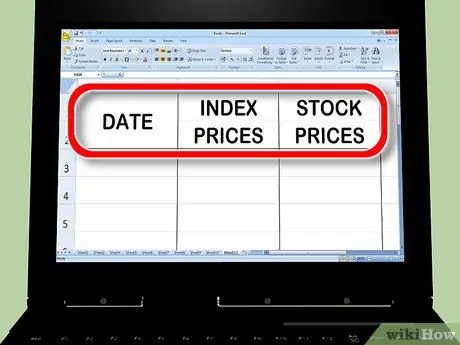
1. Hozzon létre három ároszlopot az Excelben
Az első oszlop a dátum. A második oszlopba írja be az indexárat; ez az "általános piac", amelyhez a bétákat összehasonlítja. A harmadik oszlopba írja be azt a reprezentatív részvényárat, amelyhez a bétát próbálja kiszámítani.
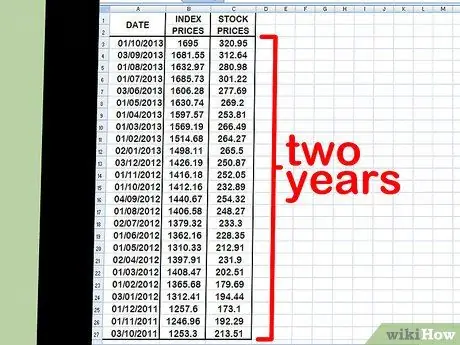
2. lépés. Helyezze az adatpontokat egy táblázatba
Próbálkozzon egy hónapos időközönként. Válasszon egy dátumot - például a hónap elején vagy végén -, és írja be a megfelelő értéket a tőzsdei indexhez (próbálja meg használni az S&P 500 -at), majd az adott napra vonatkozó részvényt. Válassza ki az utolsó 15 vagy 30 dátumot, esetleg egy -két évet a múltba. Ügyeljen az index árára és a reprezentatív részvényárfolyamra az adott napon.
Minél hosszabb időtartamot választ, annál pontosabb lesz a béta számítása. A béta változik, miközben hosszú ideig figyeli a részvényeket és az indexeket
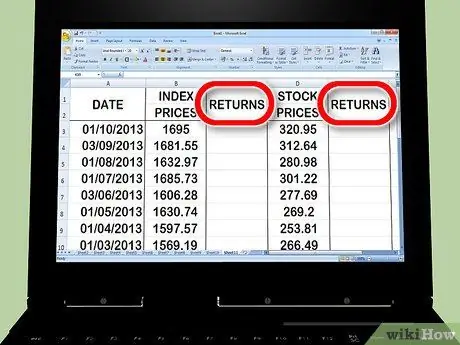
3. Hozzon létre két oszlopot az ároszlop jobb oldalán
Az egyik oszlop az indexet adja vissza; a második oszlop az állomány. Excel képletek segítségével határozza meg újra a következő lépésekben tanultakat.
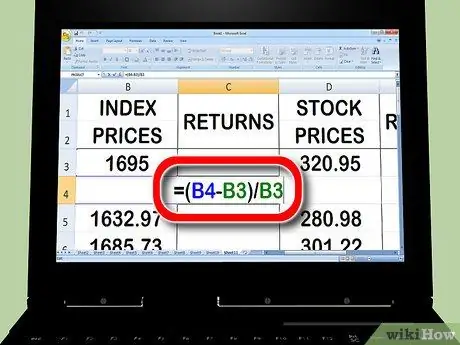
4. lépés: Kezdje vissza a részvénypiaci index számítását
Az index oszlop második cellájába írja be a =. A kurzorral kattintson az index oszlop második cellájára, írja be a -, majd kattintson az index oszlop első cellájára. Ezután írja be a / parancsot, majd kattintson ismét az index oszlop első cellájára. nyomja meg a Return vagy az Enter billentyűt.
- Ha idővel újraszámítja, semmit nem ír be az első cellába; hagyd üresen. Legalább két adatpontra van szüksége az újraszámításhoz, ezért az index oszlop második cellájából indul.
- Mit kell tennie, ha kivonja az új értéket a régi értékből, majd elosztja az eredményt a régi értékkel. Ez azért van, hogy tudja, mennyi volt a veszteség vagy nyereség százaléka az adott időszakban.
- A visszatérési oszlopban szereplő egyenlete így nézhet ki: = (B3-B2)/B2
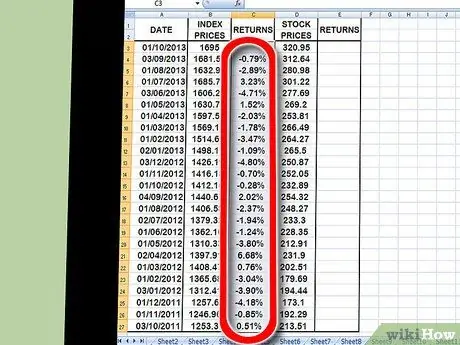
5. lépés: A másolási funkcióval ismételje meg ezt a folyamatot az indexár oszlop összes adatpontjánál
Ehhez kattintson az indexcella jobb alsó sarkában található kis négyzetre, majd húzza le a legalsó adatponthoz. Ön megkérheti az Excel -t, hogy replikálja ugyanazt a képletet, amelyet minden egyes adatponthoz használt.
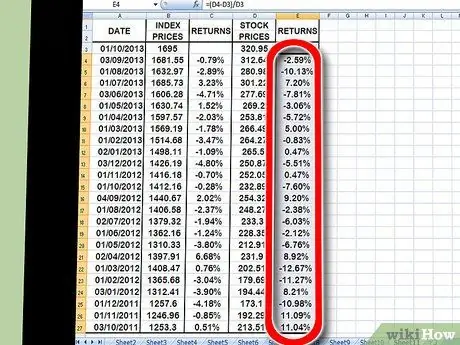
6. lépés: Ismételje meg pontosan ugyanazt a folyamatot a hozamoknál, ezúttal az egyes részvényeknél, nem pedig az indexeknél
Ha elkészült, két oszlopa van, százalékban formázva, amelyek felsorolják az egyes részvényindexek és az egyes részvények hozamait.
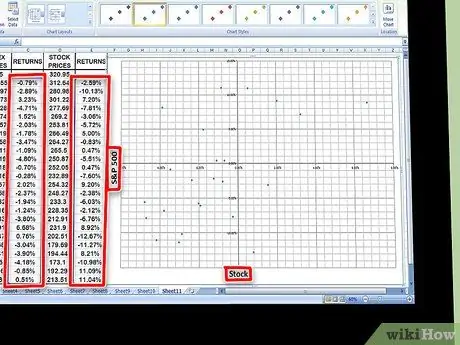
7. lépés. Ábrázolja az adatokat egy táblázatba
Jelölje ki az összes adatot a két visszatérési oszlopban, és nyomja meg a Diagram ikont az Excelben. Válassza ki a szórási grafikont a lehetőségek listájából. Nevezze az X tengelyt az Ön által használt indexnek (pl. S&P 500), az Y tengelyt pedig a használt részvénynek.
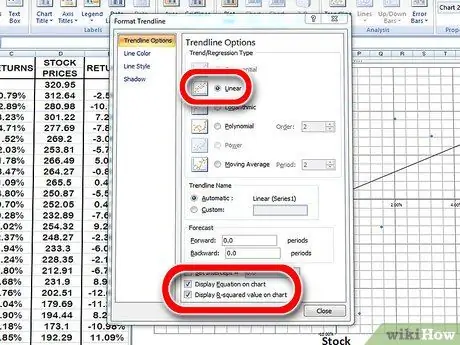
8. Trendvonal hozzáadása a szórási diagramhoz
Ezt úgy is megteheti, hogy kiválaszt egy trendvonal -elrendezést az Excel újabb verzióiban, vagy manuálisan megadja a Diagram → Trendvonal hozzáadása lehetőségre kattintva. Feltétlenül jelenítse meg az egyenletet a táblázatban. 2 értékeket.
- Győződjön meg róla, hogy lineáris trendvonalat választ, nem polinomot vagy átlagot.
- Az egyenlet táblázatban való megjelenítése attól függ, hogy milyen Excel verzióval rendelkezik. Az Excel újabb verziói lehetővé teszik az egyenletdiagramot a Diagram gyors elrendezése gombra kattintva.
- Az Excel ezen verziójában mutasson a Diagramra; Trendline hozzáadása; lehetőségek. Ezután jelölje be mindkét jelölőnégyzetet az "Egyenlet megjelenítése a diagramon" mellett.
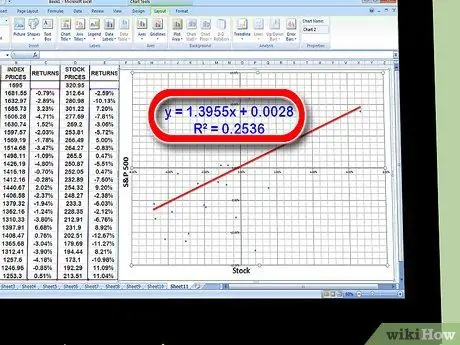
9. lépés. Keresse meg az "x" érték együtthatóját a trendvonal egyenletében
A trendvonal egyenlete "y = x + a" formában lesz írva. Az x érték együtthatója béta.
4. rész a 4 -ből: A béta megértése

1. lépés: A béta értelmezése
A béta a részvénypiac egészét fenyegető kockázat, a befektető átvállalja egy adott részvény tulajdonjogát. Ezért kell összehasonlítani az egyes részvények hozamát az index - a referenciaindex - hozamával. Az indexkockázat továbbra is 1. Az „alacsony” 1 -es béta azt jelenti, hogy a részvény kevésbé kockázatos, mint az összehasonlítandó index. A „magas” 1 -es béta azt jelenti, hogy a részvény kockázatosabb, mint az az index, amelyhez hasonlítják.
- Vegyük ezt a példát. Tegyük fel, hogy a Gino Germ bétáját 0,5 -re számítják. Az S&P 500 -hoz képest a Gino által összehasonlított benchmark "fele" kockázatos. Ha az S&P 10%alá kerül, akkor a Gino részvényárfolyama csak 5%-kal csökken.
- Másik példaként képzeljük el, hogy Frank temetkezési szolgáltatásának bétája az S&P -hez képest 1,5. Ha az S&P 10%-ot esik, számítson arra, hogy Frank részvényárfolyama "többet" fog esni, mint az S&P, vagy körülbelül 15%-kal.

2. lépés. A kockázat a hozamokhoz is kapcsolódik
Nagy kockázat, magas jutalom; alacsony kockázat, alacsony jutalom. Az alacsony bétával rendelkező részvények nem veszítenek annyit, mint az S&P, ha esnek, de nem fognak annyit nyerni, mint az S&P, ha nyereséget tesznek közzé. Másrészről, az 1 -nél béta béta részvények többet veszítenek, mint az S&P, ha esnek, de többet is nyernek, mint az S&P, amikor közzéteszik.
Például a Vermeer Venom Extraction béta értéke 0,5. Amikor a tőzsde 30% -ot ugrik, a Vermeer csak 15% -os nyereséget termel. De amikor a raktári részvénypiac 30%, Vermeer csak 15% -os raktári készletet kap

Lépés 3. Tudja, hogy a béta 1 -es részvények a piaccal összhangban mozognak
Ha béta számítást végez, és ismeri a részvényt, elemzi, hogy mikor van béta 1, akkor nem lesz több vagy kevesebb kockázat, mint az összehasonlításként használt index. A piac 2%-ot, a részvénye 2%-ot emelkedett; a piac 8%-os mínuszban van, a részvényei 8%-kal.
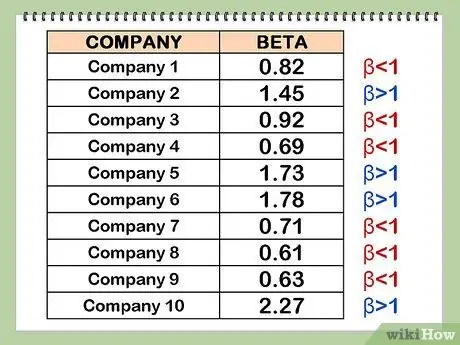
Lépés 4. A diverzifikáció érdekében vegye fel portfóliójába mind a magas, mind az alacsony béta -részvényeket
Ha a magas és a mélypont jó keveréke, a béta segít elemezni, hogy a tőzsdei érték drasztikusan csökken -e. Természetesen, mivel az alacsony béta-részvények általában alulteljesítik a teljes tőzsdét egy adott időszakban, a béták jó keveréke azt is jelenti, hogy nem fogja tapasztalni, hogy a részvényárfolyam különösen magas lesz.

5. Lépés. Ismerje fel, hogy a legtöbb pénzügyi előrejelző eszközhöz hasonlóan a béták sem tudják előre megjósolni a jövőt
A béta valójában egy részvény múltbeli volatilitását méri. Általában a projektek a jövőre volatilitást jelentenek, de nem mindig pontosak. A béta egyik évről a másikra drasztikusan megváltozhat. A részvények korábbi bétájának használata nem mindig lehet pontos módszer a jelenlegi volatilitás előrejelzésére.
Javaslat
- Ne feledje, hogy a klasszikus kovariancia -elmélet a Heavy tail pénzügyi idősor miatt nem alkalmazható”. Valójában előfordulhat, hogy az alapeloszlás szórása és átlaga nem létezik! Tehát talán az átlag és a szórás helyett kvartilis és medián spreadeket használó módosítás működhet.
- A béta elemzi a részvények volatilitását egy bizonyos idő alatt, függetlenül attól, hogy a piac felfelé vagy lefelé van -e. Más részvényalapokhoz hasonlóan a múltbeli teljesítmény elemzése sem garancia arra, hogy a részvény hogyan fog teljesíteni a jövőben.






