A keresztszorzás a két egyenértékű tört változóját tartalmazó egyenletek megoldásának módja. A változó ismeretlen számú szám helyőrzője, és a keresztszorzás egyszerű egyenletké alakítja, lehetővé téve a kérdéses változó értékének megtalálását. A keresztszorzás nagyon hasznos, ha összehasonlítást szeretne végezni. Ezt a következőképpen teheti meg:
Lépés
1 /2. Módszer: Egy változó keresztterméke
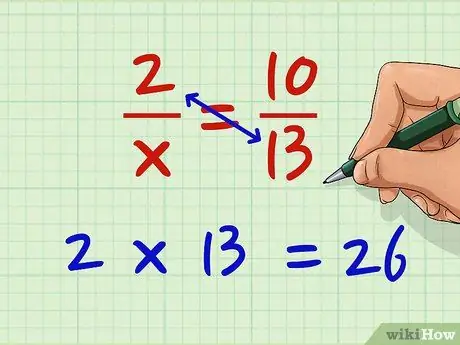
1. lépés Szorozzuk meg a bal oldali tört számlálóját a jobb oldali tört nevezőjével
Tegyük fel, hogy meg szeretné oldani a 2/x = 10/13 egyenletet. Most szorozzuk meg a 2 -t 13,2 x 13 = 26 -mal.
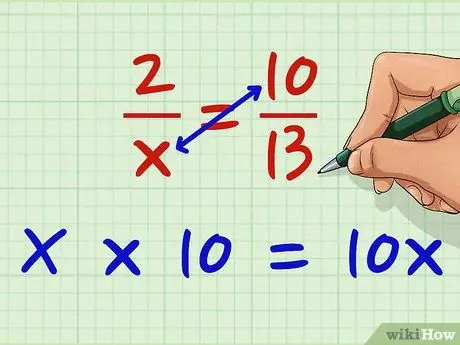
2. lépés Szorozzuk meg a jobb oldali nevezőt a bal oldali nevezővel
Szorozzuk meg x -et 10 -gyel. X * 10 = 10x. Először átlépheti ezt a szakaszt; nem számít, amíg mindkét számlálót átlósan megszorozzuk mindkét nevezővel.
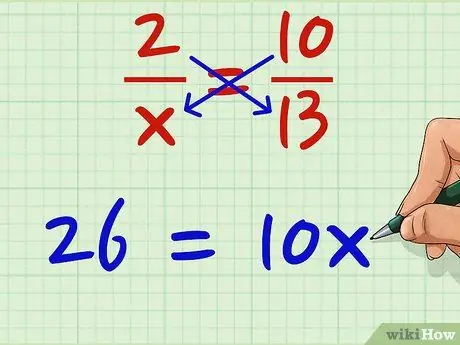
3. lépés: A két terméket egyenlővé kell tenni
26 10x -nek felel meg. 26 = 10x. Mindegy, hogy melyik a jobb vagy a bal; mivel egyenlő, megváltoztathatja a helyüket, ha egyszerre mozgatja őket.
Tehát ha megpróbálja megtalálni a 2/x = 10/13 x értékét, 2 * 13 = x * 10 vagy 26 = 10x
4. lépés Keresse meg a változó értékét
Most, hogy 26 = 10x, megpróbálhat közös számlálót találni, és a 26 -ot és a 10 -et eloszthatja ugyanazzal a számmal, amely osztja mindkettőt. Mivel mindkettő páros szám, oszthatja 2 -vel; 26/2 = 13 és 10/2 = 5. A maradék 13 = 5x. Most, ha egyedül x -et veszünk, osszuk el az egyenlet mindkét oldalát 5 -tel. Tehát 13/5 = 5/5 vagy 13/5 = x. Ha tizedes formában szeretné megválaszolni a választ, akkor először az egyenlet mindkét oldalát el kell osztani 10 -gyel, így 26/10 = 10/10 vagy 2,6 = x.
2. módszer 2 -ből: Többváltozós keresztszorzás
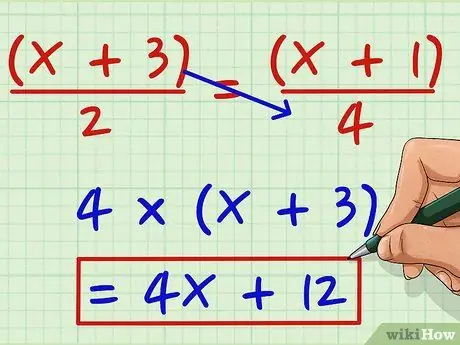
1. lépés Szorozzuk meg a bal oldali számlálót a jobb oldali nevezővel
Tegyük fel, hogy a következő egyenletet szeretné megoldani: (x + 3)/2 = (x + 1)/4. Szorozzuk meg (x + 3) 4 -gyel, hogy 4 -et kapjunk (x + 3). Szorozzuk meg 4 -gyel, hogy 4x + 12 -et kapjunk.
2. lépés Szorozzuk meg a jobb oldali számlálót a bal oldali nevezővel
Ismételje meg a folyamatot a másik oldalon. (x+1) x 2 = 2 (x+1). Szorozd meg 2 -vel, hogy 2x + 2 -t kapj.
3. lépés Tegye egyenlővé a két szorzatát, és egyesítse ugyanazokat a változókat
Most az eredmény 4x + 12 = 2x + 2. Kombinálja az x változót és az egyenletet az egyenlet másik oldalán.
- Tehát kombinálja a 4x és 2x kétszer úgy, hogy mindkét oldalról 2x kivon. Ha 2x kivonunk 2x -ből, akkor a maradék 0 marad. A bal oldalon 4x - 2x = 2x, tehát a maradék 2x.
- Most egyesítse a 12 -t és a 2 -t úgy, hogy levonja a 12 -t mindkét oldalról. A bal oldali 12 -ből vonja le a 12 -t, és az eredmény 0, majd a jobb oldali 2 -ből vonja le a 12 -t, hogy az eredmény 2 -12 = -10 legyen.
- A maradék 2x = -10.
4. lépés. Befejezés
Nincs más dolgod, mint elosztani az egyenlet mindkét oldalát 2 -vel. 2x/2 = -10/2 = x = -5. A keresztszorzás után azt találjuk, hogy x = -5. Visszatérhet, és ellenőrizheti munkáját, ha megadja az x értékét, ami -5, hogy megbizonyosodjon arról, hogy mindkét oldal egyenlő. Kiderült, hogy egyenértékű. Ha a -5 -öt csatlakoztatja az eredeti egyenlethez, az eredmény -1 = -1.
Tippek
- Ne feledje, hogy ha különböző számokat (mondjuk 5 -öt) csatlakoztat egyazon egyenlethez, az eredmény 2/5 = 10/13. Még akkor is, ha a bal oldalt megszorozzuk egy másik 5/5 -tel, akkor 10/25 = 10/13 értéket kapunk, ami egyértelműen helytelen. Ez az eset azt jelzi, hogy keresztszorzási hibát követett el.
- Ellenőrizheti válaszát, ha az eredményt az eredeti egyenletbe illeszti. Ha az egyenlet igaz állítás, például 1 = 1, akkor a válasz helyes. Ha az egyenlet hamis állítássá válik, például 0 = 1, akkor hibát követett el. Például dugja be a 2, 6 -ot az egyenletbe úgy, hogy 2/(2, 6) = 10/13. Szorozzuk meg a bal oldalt 5/5 -tel, hogy 10/13 = 10/13 legyen. Az eredmény egy helyes állítás, amely egyszerűsítve 1 = 1 lesz, tehát 2, 6 a helyes válasz.
