- Szerző Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:16.
- Utoljára módosítva 2025-01-23 12:20.
A gravitáció a fizika egyik alapvető ereje. A gravitáció legfontosabb aspektusa, hogy univerzális: minden tárgy gravitációs erővel vonzza a többi tárgyat. A gravitációs erő nagysága függ a két tárgy tömegétől és távolságától.
Lépés
Rész 1 /2: A gravitációs erő kiszámítása két tárgy között

1. lépés. Határozza meg az objektumra ható gravitációs erő egyenletét, Fgrav = (Gm1m2)/d2.
Az objektum gravitációs erejének kiszámításához ez az egyenlet figyelembe veszi a két tárgy tömegét és távolságát is. Az egyenletváltozókat az alábbiakban ismertetjük.
- Fgrav a gravitációs erő
- G az univerzális gravitációs állandó 6,673 x 10-11 Nm2/kg2
- m1 az első tárgy tömege
- m2 a második tárgy tömege
- d a két objektum középpontja közötti távolság
- Néha d helyett r betűt talál. Ez a két szimbólum a két objektum közötti távolságot jelöli.

2. lépés. Használja a megfelelő metrikus egységeket
Ehhez az egyenlethez metrikus egységeket kell használnia. A tárgy tömegének kilogrammban (kg) és a tárgyak közötti távolságnak méterben (m) kell lennie. A folytatás előtt ezeket az egységeket metrikus egységekké kell alakítania

3. lépés. Határozza meg a kérdéses tárgy tömegét
Kisméretű tárgyak esetén mérlegelve meghatározhatja súlyukat kilogrammban. Nagyméretű tárgyak esetén a táblázatban vagy az interneten megkeresheti a hozzávetőleges tömeget. Fizikai feladatokban általában az objektum tömegét mondják meg.

4. lépés. Mérje meg a távolságot a két objektum között
Ha megpróbálja kiszámítani a gravitációs erőt egy tárgy és a föld között, tudnia kell, hogy ez az objektum milyen messze van a föld középpontjától.
- A földfelszín és a középpont közötti távolság körülbelül 6,38 x 106 m.
- Kereshet táblázatokat vagy más forrásokat az interneten, amelyek megmondják, hogy a Föld középpontja milyen távolságban van a földfelszín különböző magasságú tárgyaitól.

5. lépés Végezze el a számítást
Ha meghatározta a változókat az egyenletben, bátran írja be őket a megoldáshoz. Győződjön meg arról, hogy minden változó metrikus egységekben van, és megfelelően méretezett. A tömegnek kilogrammban, a távolságnak méterben kell lennie. Oldja meg az egyenleteket a helyes számítási sorrendben.
- Például határozza meg annak a személynek a gravitációs erejét, akinek tömege 68 kg a földfelszín felett. A Föld tömege 5,98 x 1024 kg.
- Győződjön meg arról, hogy minden változó helyes mértékegységben van. m1 = 5, 98 x 1024 kg, m2 = 68 kg, G = 6,673 x 10-11 Nm2/kg2és d = 6, 38 x 106 m
- Írd fel az egyenletet: F.grav = (Gm1m2)/d2 = [(6, 67 x 10-11) x 68 x (5, 98 x 1024)]/(6, 38 x 106)2
- Szorozzuk meg a figyelembe vett két objektum tömegét. 68 x (5, 98 x 1024) = 4,06 x 1026
- Szorozzuk meg az eredményt m1 és M2 G gravitációs állandóval. (4,06 x 1026) x (6,67 x 10-11) = 2,708 x 1016
- Tegye négyzetre a két tárgy közötti távolságot. (6, 38 x 106)2 = 4,07 x 1013
- Eredmény megosztása G x m1 x m2 a távolság négyzetével, hogy megkapjuk a gravitációs erőt Newtonban (N). 2, 708 x 1016/4, 07 x 1013 = 665 N
- Gravitációs ereje 665 N.
2/2. Rész: A gravitációs erő kiszámítása a Földön

1. lépés. Ismerje meg Newton második törvényét, F = ma
Newton második törvénye kimondja, hogy egy tárgy gyorsulása egyenesen arányos a rá ható nettó erővel, és fordítottan arányos a tömegével. Más szóval, ha egy tárgyra ható erő nagyobb, mint az ellenkező irányba ható erő, akkor a tárgy az erősebb erővel mozog.
- Ezt a törvényt össze lehet foglalni az F = ma egyenlettel, ahol F az erő, m a tárgy tömege és a a gyorsulás.
- Ennek a törvénynek köszönhetően kiszámíthatjuk a Föld felszínén lévő összes tárgy gravitációs erejét, a gravitáció miatti ismert gyorsulás segítségével.
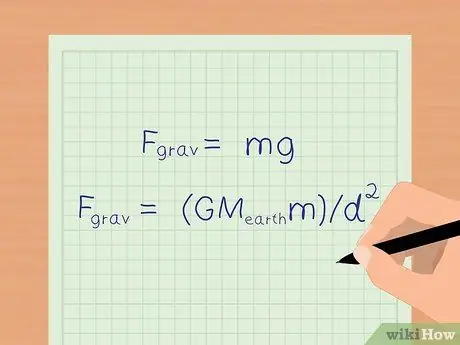
2. lépés. Keresse meg a Föld gravitációjának köszönhető gyorsulást
A földön a gravitációs erő hatására minden tárgy 9,8 m/s sebességgel gyorsul2. A föld felszínén használhatunk egy egyszerűsített egyenletet: Fgrav = mg a gravitációs erő kiszámításához.
Ha pontosabb gravitációs erők számát szeretné tudni, akkor is használhatja az előző lépésben szereplő képletet, Fgrav = (GMföldm)/d2 a gravitációs erő meghatározásához.

3. lépés. Használja a megfelelő metrikus egységeket
Ehhez az egyenlethez metrikus egységeket kell használnia. A tárgy tömegének kilogrammban (kg) és a tárgyak közötti távolságnak méterben (m) kell lennie. A folytatás előtt ezeket az egységeket metrikus egységekké kell konvertálnia.

4. lépés. Határozza meg a tárgy tárgyát
Kisméretű tárgyak esetén mérlegelve meghatározhatja súlyukat kilogrammban. Nagyméretű tárgyak esetén a táblázatban vagy az interneten megkeresheti a hozzávetőleges tömeget. Fizikai feladatokban általában az objektum tömegét mondják meg.

5. lépés Végezze el a számítást
Ha meghatározta a változókat az egyenletben, bátran írja be őket a megoldáshoz. Győződjön meg arról, hogy minden változó metrikus egységekben van, és megfelelően méretezett. A tömegnek kilogrammban, a távolságnak méterben kell lennie. Oldja meg az egyenleteket a helyes számítási sorrendben.
- Próbáljuk meg használni az előző lépésben szereplő egyenletet, és nézzük meg, milyen közel vannak az eredmények. Határozza meg a 68 kg tömegű személy gravitációs erejét a föld felszínén.
- Győződjön meg arról, hogy minden változó helyes mértékegységben van: m = 68 kg, g = 9,8 m/s2.
- Írja le a képletet. Fgrav = mg = 68*9, 8 = 666 N.
- Az F = mg képlet használatával a gravitációs erő 666 N, míg az előző lépésben kapott képlet eredménye 665 N. Mint látható, a két eredmény majdnem ugyanaz.
Tippek
- Ennek a két képletnek ugyanazt a választ kell adnia, de a rövidebb és egyszerűbb képletet könnyebb használni, ha a bolygó felszínén lévő tárgyakat tárgyaljuk.
- Használja az első képletet, ha nem ismeri a bolygó gravitációjának köszönhető gyorsulást, vagy két nagyon nagy tárgy, például a Hold vagy a bolygók közötti gravitációs erőt számítja ki.






