Az IQR egy adathalmaz interkvartilis tartománya vagy kvartilis gyökér tartománya. Az IQR -t statisztikai elemzésben használják, hogy segítsenek következtetéseket levonni egy adathalmazra vonatkozóan. Az IQR -t gyakrabban használják, mint a tartományt, mert az IQR nem tartalmazza a legkülső adatokat. Folytassa az olvasást, hogy megtudja, hogyan találja meg az IQR -t!
Lépés
Módszer 1 /3: Az IQR megértése
1. lépés: Ismerje meg az IQR használatát
Alapvetően az IQR egy módja annak, hogy megértsük egy számhalmaz terjedését. A gyökér kvartilis tartomány az adathalmaz felső kvartilisének (25% felső) és az alsó kvartilis (25% legalacsonyabb) közötti különbsége.
Tipp:
Az alsó kvartilis általában Q1, a felső kvartilis pedig Q3 - ami technikailag az adatok felezőpontját Q2 -re, a legmagasabb pontot pedig Q4 -re teszi.
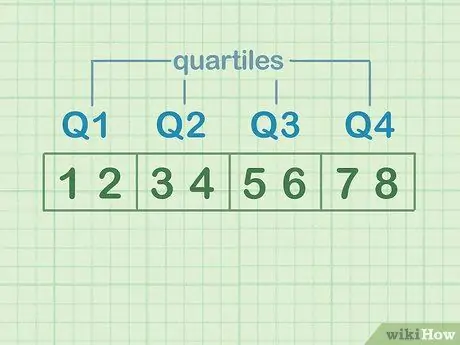
2. lépés. Értse meg a kvartiliseket
A kvartilisek szemléltetésére ossza a számhalmazt négy egyenlő részre. Ezen részek mindegyike „kvartilis”. Tegyük fel, hogy az adatkészletek a következők: 1, 2, 3, 4, 5, 6, 7, 8.
- Az 1. és 2. az első kvartilis vagy Q1
- A 3. és 4. ábra a második kvartilis vagy Q2
- 5. és 6. a harmadik kvartilis vagy Q3
- A 7. és 8. a negyedik kvartilis vagy Q4
3. lépés. Ismerje meg a képletet
Ahhoz, hogy megtalálja a különbséget a felső és az alsó kvartilis között, ki kell vonnia a 75. percentilt a 25. percentilisből.
A képlet a következő: Q3 - Q1 = IQR
2. módszer a 3 -ból: Az adathalmaz összeállítása
1. lépés: Gyűjtse össze adatait
Ha az IQR -t az osztályban és a tesztekben tanulmányozza, akkor egy előre elkészített adatkészletet kaphat, például 1, 4, 5, 7, 10. Ez az Ön adatkészlete - a számok, amelyekkel dolgozni fog. Saját számokat azonban felépíthet asztali kérdésekből vagy történetproblémákból.
Győződjön meg arról, hogy minden szám ugyanazt jelenti:
például egy meghatározott madárpopuláció minden fészekében lévő tojások száma, vagy egy meghatározott tömb minden házában található parkolóhelyek száma.
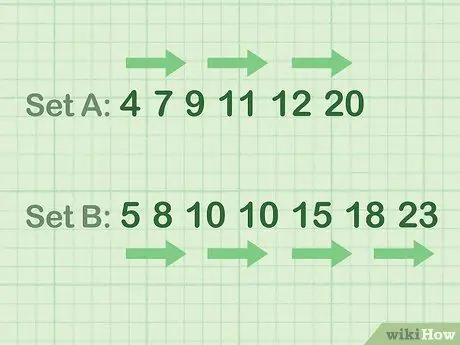
Lépés 2. Rendezze az adatokat növekvő sorrendbe
Más szóval: rendezze a számokat a legkisebbtől a legnagyobbig. Használja a következő példákból származó tippeket.
- Példa páros számadatokra (A halmaz): 4 7 9 11 12 20
- Példa páratlan számadatokra (B készlet): 5 8 10 10 15 18 23
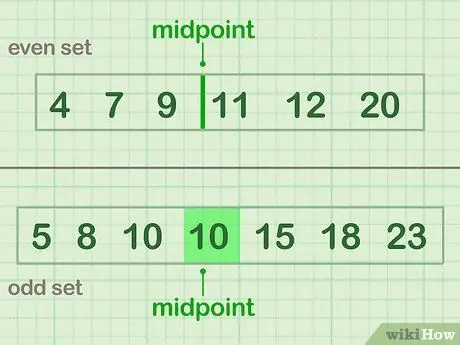
Lépés 3. Ossza fel az adatokat két részre
A felére bontáshoz keresse meg az adatok felezőpontját: azt a számot vagy számokat, amelyek az adathalmaz közepén vannak. Ha páratlan számú adat áll rendelkezésre, válassza ki a középen lévő számot. Ha páros adatokkal rendelkezik, akkor a felezőpont a két középső szám között van.
- Egy páros példa (A halmaz), amelynek középpontja 9 és 11 között van: 4 7 9 | 11 12 20
- Egy páratlan példa (B halmaz), amelynek középpontja (10): 5 8 10 (10) 15 18 23
3. módszer 3 -ból: Az IQR kiszámítása
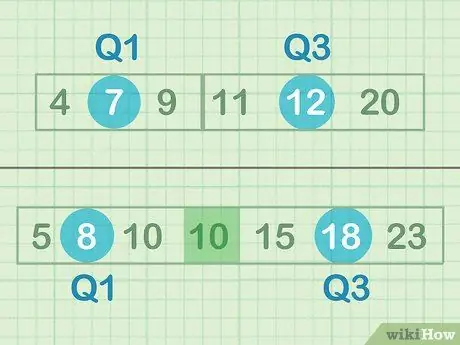
1. lépés. Keresse meg az adatok alsó és felső felének mediánját
A medián a "középső pont" vagy szám, amely a számhalmaz közepén található. Ebben az esetben nem az összes szám középpontját keresi, hanem a felső és az alsó adathalmaz relatív középpontját. Ha páratlan számú adat áll rendelkezésre, ne adja meg a középső számot - például a B készletben nem kell egyetlen 10 -et sem megadnia.
-
Még példa (A halmaz):
- Az adatok alsó felének mediánja = 7 (Q1)
- Az adatok felső felének mediánja = 12 (Q3)
-
Furcsa példa (B halmaz):
- Az adatok alsó felének mediánja = 8 (Q1)
- Az adatok felső felének mediánja = 18 (Q3)
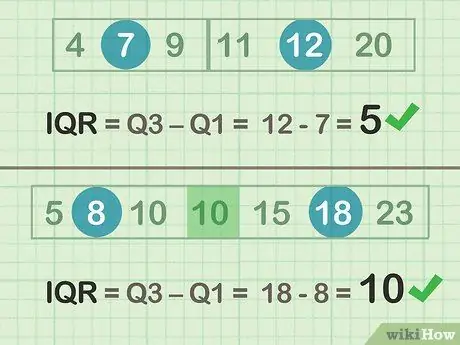
2. lépés Vonja le a Q3-Q1-et az IQR meghatározásához
Most már tudja, hány szám esik a 25. és a 75. százalék közé. Ezzel a számmal megértheti az adatok terjedését. Például, ha egy teszt maximális pontszáma 100, és az eredmény IQR értéke 5, akkor feltételezheti, hogy a legtöbb tesztet végző ember közel azonos a megértéssel, mert a csúcsok és mélypontok tartománya nem túl nagy. Ha azonban a teszt eredményének IQR értéke 30, akkor azon tűnődhet, hogy egyesek miért olyan magasak, mások miért olyan alacsonyak.
- Pár példa (A halmaz): 12 -7 = 5
- Páratlan példa (B halmaz): 18 - 8 = 10
Tippek
Fontos, hogy megtanulja ezt egyedül csinálni. Számos online IQR számológép létezik azonban, amelyekkel ellenőrizheti munkáját. Ne hagyatkozzon túl sokat a számológépes alkalmazásokra, ha ezt az órán megtanulja! Ha megkérik, hogy keresse meg az IQR -t egy tesztben, tudnia kell, hogyan kell manuálisan megtalálni
Kapcsolódó WikiHow
- Hogyan lehet észlelni a kiugró értékeket
- Hogyan kell kiszámítani az adathalmaz tartományát?
- Hogyan készítsünk egy dobozt és sátor diagramot
