- Szerző Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:13.
- Utoljára módosítva 2025-01-23 12:20.
A négyzet hüvelyk meghatározásának folyamata (írva, mint2) a kétdimenziós ábrák minden területén általában meglehetősen egyszerűek. A legegyszerűbb esetben, ha az ábra négyzet vagy négyszög, a hüvelykben négyzetméteres területet a képlet segítségével kaphatjuk meg hossz × szélesség.
Más síkformák (körök, háromszögek stb.) Területeit különböző matematikai képletekkel lehet kiszámítani. Szükség esetén elvégezheti a lábak négyzet vagy négyzet centiméterek egyszerű átalakítását is.
Lépés
1. módszer a 3 -ból: Négyzet hüvelyk meghatározása négyzeten vagy téren
1. lépés Határozza meg a mérendő terület hosszát
A négyzeteknek és téglalapoknak 4 egyenes oldala van. Egy négyzetnek négy oldala azonos hosszúságú, míg egy téglalapban csak a szemközti oldalak azonos hosszúságúak. Mérje meg a négyzet vagy téglalap egyik oldalát, hogy megtudja a hossz értékét.
2. lépés Határozza meg a mérendő terület szélességét
Ezután mérje meg az egyik oldalt a korábban mért oldal mellett. Ennek az oldalnak 90 fokos szögben kell találkoznia az első oldallal. Ez a négyzet vagy téglalap szélessége.
Mivel a négyzet mind a négy oldala azonos hosszúságú, a kapott "hossz" megegyezik a "szélesség" mértékével. Tehát általában egy négyzethez csak az egyik oldalát kell megmérni
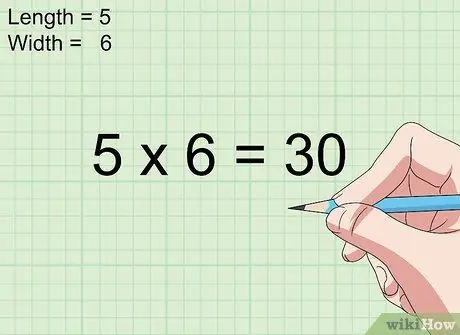
3. lépés Szorozza meg a hosszúságot és a szélességet
Egyszerűen szorozza meg a hossz- és szélességméréseket, hogy meghatározza egy négyzet vagy téglalap területét hüvelyk négyzetben.
- Tegyük fel például, hogy a probléma egy 4 hüvelyk hosszú és 3 hüvelyk széles téglalap területét kéri. Ebben az esetben a téglalap területe 4 x 3 = 12 hüvelyk négyzet.
- A négyzet minden oldala ugyanolyan oldalhosszúságú. Tehát csak az egyik oldalt kell megmérnie, és meg kell szoroznia magával a számmal (más néven "négyzet" vagy kettő hatására), hogy a területet hüvelykben négyzetméterenként kapja meg.
2. módszer a 3 -ból: Négyzethüvelyk meghatározása más lapos formákon
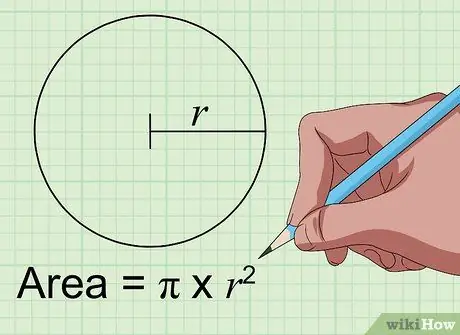
1. lépés Keresse meg a kör területét a Area = pi × r képlet segítségével2.
Ahhoz, hogy egy kör területét hüvelykben négyzetben találja meg, csak a kör középpontjától az oldalaihoz mért távolságot kell megtudnia hüvelykben. Ezt a távolságot a kör "sugarának" nevezik. Ha megkapta, egyszerűen írja be a számot a fenti képlet "r" változójába. Szorozzuk meg magával a számmal, majd szorozzuk meg a pi konstanssal (3, 1415926…), hogy megkapjuk a kör területét hüvelyk négyzetben.
Tehát egy 4 hüvelyk sugarú kör területe 50,27 hüvelyk négyzet, ami a 3,14 x 16 szorzatának szorzata
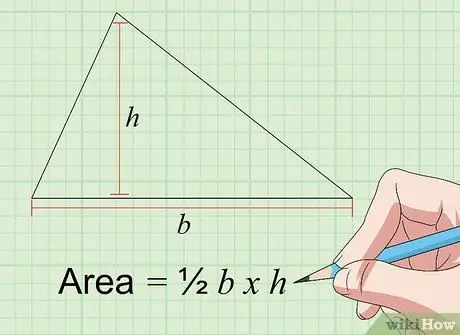
2. lépés Keresse meg a háromszög területét a Area = 1/2 a × t képlet segítségével
A háromszög területe hüvelykben négyzetben megtalálható, ha megszorozzuk az alapot ("a") és a magasságot ("t"), mindkettőt hüvelykben. A háromszög alapja az egyik oldala hossza, míg a háromszög "magassága" az "alap" oldalának és a vele szemben lévő háromszög 90 ° -os szögben lévő sarkának távolsága. A háromszög területe kiszámítható, ha ismeri az alap oldalainak hosszát és a három oldal magasságát, valamint a velük szemben lévő szögeket.
Így, ha olyan oldalt választ, amely 4 hüvelyk hosszú, mint az alap, és az alap oldalának magassága 3 hüvelyk, akkor a háromszög területe 2 x 3 = 6 hüvelyk négyzet
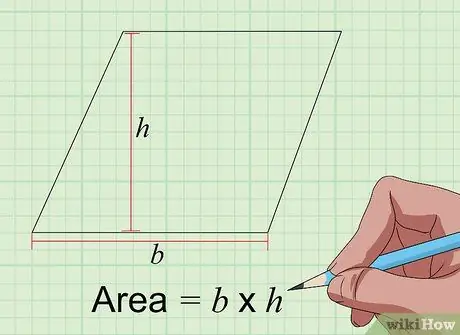
3. lépés Keresse meg a paralelogramma területét a Area = a × t képlettel
A paralelogramma hasonló a téglalaphoz, de az oldalak nem találkoznak 90 fokos szögben. Azonban a paralelogramma területének hüvelykben négyzetben történő megkeresése megegyezik a téglalapéval, ha megszorozzuk az alapot a hüvelyk magasságával. Az alap az egyik oldala hossza, míg a magasság az alap oldalától a szemközti oldalig mért távolság 90 fokos szögben.
Ezért ha a kiválasztott oldal hossza 5 hüvelyk, és a magasság mérése után 4 hüvelyk hosszú, akkor a terület 5 x 4 = 20 hüvelyk négyzet
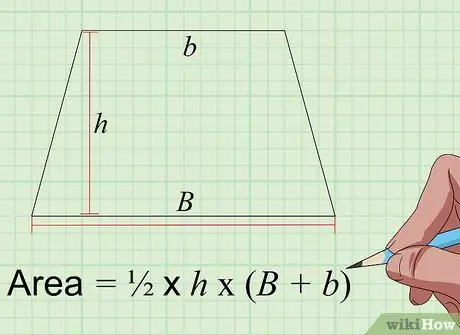
4. lépés Keresse meg a trapéz területét a Area = 1/2 × t × (A+a) képlet segítségével
A trapéz egy négyoldalas lapos forma, amelynek egyik párhuzamos oldala és a másik nem párhuzamos oldala. A trapéz területének hüvelykben négyzetben történő kiszámításához ismernie kell 3 hüvelykben mért mérést, a hosszú párhuzamos oldal („A”), a rövidebb párhuzamos oldal („a”) hosszát és magasságát. a trapézból („t”)., azaz két párhuzamos oldal közötti távolság 90 fokos szögben mérve. Adja hozzá a két párhuzamos oldal hosszát, szorozza meg a magassággal, majd ossza el kettővel, hogy megkapja a trapéz területét hüvelykben négyzetben.
Például, ha egy trapéz párhuzamos oldalai 6 hüvelyk hosszúak, a rövid párhuzamos oldalak 4 hüvelyk, a magasság pedig 5 hüvelyk, akkor a terület x 5 x (6+4) = 25 négyzet hüvelyk
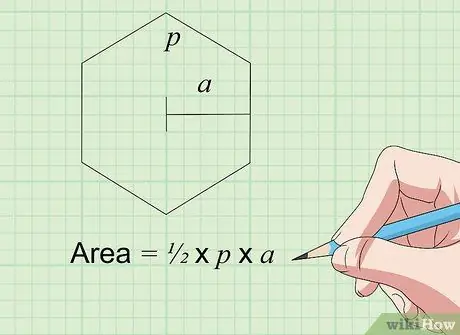
5. lépés Keresse meg a hatszög (hatszög) területét a Area = × K × s képlettel
Ez a képlet minden szabályos hatszögre vonatkozik, amelyek laposak, 6 egyenlő oldalú és 6 egyenlő szögű. K a kerülete, vagy az oldalhossz 6 -szor (6 x s) egy szabályos hatszög esetén. Az a változó az apotémát jelenti, amely a hatszög középpontjától az egyik oldaláig terjedő hossz (a két szög közötti oldal felezőpontja). Szorozzuk és osszuk el az eredményt, hogy megtaláljuk a hatszög területét.
Így ha egy hatszög, amelynek mind a hat oldala 4 hüvelyk hosszú (ez azt jelenti, hogy K = 6 x 4 = 24), és az apotéma 3,5 hüvelyk hosszú, a terület x 24 x 3,5 = 42 négyzet hüvelyk
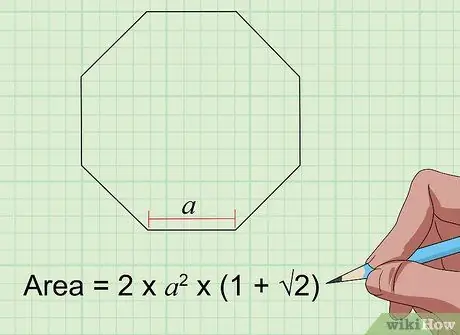
6. lépés Keresse meg a nyolcszög területét a Area = 2s² × (1 + 2) képlettel
Egy szabályos nyolcszög esetén (amelynek 8 egyenlő oldala és 8 szöge van), csak a terület megkereséséhez kell ismernie az egyik oldal hosszát („s”). Csatlakoztassa az értékeket a képlethez, és dolgozza ki őket, hogy megkapja a nyolcszög területét.
Ha a szokásos nyolcszög oldalhossza 4 hüvelyk, területe 2 (16) x (1 + 1, 4) = 32 x 2,4 = 76,8 négyzet hüvelyk
3. módszer 3 -ból: Más egységek átalakítása négyzethüvelykre

1. lépés Számítás előtt módosítsa a méretet hüvelykre
Ha végső választ szeretne négyzet hüvelykben megadni, javasoljuk, hogy az összes számítandó értéket alakítsa át hüvelykre (például hossz, magasság vagy apotéma). Így ha a négyzet oldalai egyenként 1 láb hosszúak, akkor a terület kiszámítása előtt alakítsák át 12 hüvelykre. A hüvelykre való átváltáshoz általában a következő konverziós tényezőket használják:
- 1 láb = 12 hüvelyk
- 1 yard = 36 hüvelyk
- 1 centiméter = 0,3937 hüvelyk
- 1 méter = 39.3701 hüvelyk
- 1 milliméter = 0,0394 hüvelyk
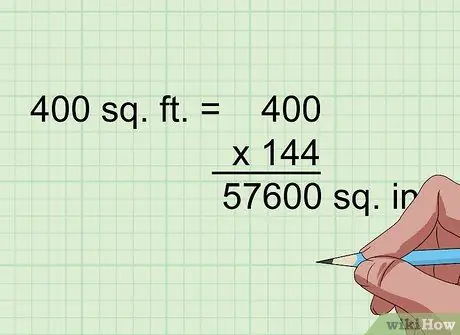
2. lépés: Szorozzuk meg 144 -gyel, hogy a négyzetlábakat négyzet hüvelykre alakítsuk át
1 láb négyzet 1 láb négyzet (1 láb szor 1 láb); ami azt jelenti, hogy a 12 hüvelyk négyzet is egyenlő 12 hüvelyk és 12 hüvelyk szorzásával, ami 144 hüvelyk négyzetet jelent. Tehát, ha egy lapos alakzatnak négyzetméteres lába van, egyszerűen szorozza meg 144 -gyel, hogy hüvelyk négyzetre alakítsa át.
Például 400 láb négyzetben = 400 x 144 = 57 600 hüvelyk négyzet
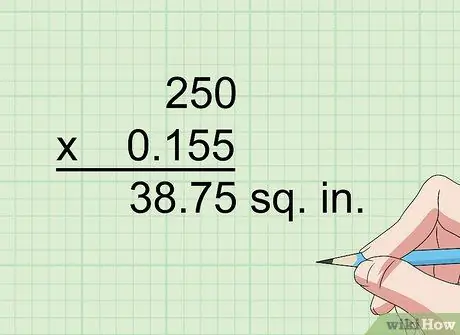
Lépés 3. Szorozza meg 0,155 -tel, hogy a négyzetcentimétereket négyzet hüvelykre alakítsa át
Egy centiméter 0,394 hüvelyk, 0,394 négyzet (0,394 x 0,394) pedig 0,155. Így például, ha 250 centimétert négyzetméterenként hüvelykre kell konvertálnia, szorozza meg 250 -et 0,155 -vel, hogy 38,75 hüvelyk négyzetet kapjon.






