- Szerző Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:13.
- Utoljára módosítva 2025-01-23 12:20.
Mindenki megtanulhatja a matematikát, függetlenül attól, hogy már magasabb iskolai stádiumban van, vagy csak újra szeretné csiszolni az alapokat. Miután megbeszéltük, hogyan lehet jó tanuló a matematikában, ez a cikk megtanítja az alapvető matematikai haladásokat, és megadja azokat az alapvető elemeket, amelyeket meg kell tanulnia minden gyakorlatban. Ezután ez a cikk a számtan tanulásának alapjait tárgyalja, amely mind az általános iskolás gyerekeknek, mind pedig mindazoknak segíteni fog, akik szeretnék elsajátítani ennek a tudományterületnek az alapjait.
Lépés
1. rész a 6 -ból: Kulcsok a jó matematika tanulóvá váláshoz

1. lépés. Jelenjen meg az osztályban
Ha elmulasztja az órát, akkor fogalmakat kell tanulnia az osztálytársaitól vagy a tankönyvéből. Soha nem kapsz szöveges összefoglalót egy barátodtól, mint a tanárodtól.
- Gyere időben az órára. Ehelyett érkezzen egy kicsit korán, és nyissa ki a jegyzetfüzetét a megfelelő helyen, nyissa ki a tankönyvet, és vegye elő a számológépet, hogy készen álljon a kezdésre, amikor a tanár készen áll a tanításra.
- Csak hanyagoljon, ha beteg. Ha nagyon hiányzik az óra, kérje meg osztálytársait, hogy derítsék ki, miről beszél a tanár, és milyen házi feladatot adtak.

2. lépés. Dolgozzon együtt tanárával
Ha a tanár az osztály előtt dolgozik egy problémán, dolgozzon együtt a tanárral úgy, hogy a problémát a füzetében dolgozza fel.
- Győződjön meg arról, hogy jegyzetei világosak és könnyen olvashatók. Ne csak kérdéseket írjon. Írjon le mindent, amit a tanár mond, ami javíthatja a magyarázott fogalmak megértését.
- Töltse ki a tanár által adott mintakérdéseket! Miközben a tanár sétál az osztályban, miközben dolgozik, válaszoljon a feltett kérdésekre.
- Vegyen részt, ha a tanár megold egy problémát. Ne várja meg, amíg a tanár felhív. Ajánlja fel a választ, ha tudja a választ, és emelje fel a kezét, és tegyen fel kérdést, ha bizonytalan a tanított anyagban.

Lépés 3. Végezze el házi feladatát ugyanazon a napon, amikor a házi feladatot megadta
Ha ugyanazon a napon elvégzi a házi feladatot, a koncepció még mindig friss. Néha nem lehetséges ugyanazon a napon befejezni a házi feladatot. Győződjön meg arról, hogy a házi feladata elkészült, mielőtt az órára megy.

4. Lépés az órán kívül, ha segítségre van szüksége
Látogassa meg tanárát szünetekben vagy hivatali időben.
- Ha van matekközpontja az iskolában, tájékozódjon a nyitvatartásáról, és kérjen segítséget.
- Csatlakozzon egy tanulmányi csoporthoz. Egy jó tanulmányi csoport általában 4 vagy 5 emberből áll, akik különböző képességekkel rendelkeznek. Ha "C" tanuló matematikából, csatlakozzon egy 2 vagy 3 fős "A" vagy "B" osztályú diákok csoportjához, hogy javítsa készségeit. Ne csatlakozzon olyan diákok csoportjához, akiknek az osztályzata alacsonyabb, mint a tiéd.
2. rész a 6 -ból: Matematika tanulása az iskolában

1. lépés: Kezdje a számtannal
A legtöbb iskolában a diákok az általános iskolában tanulnak számtant. Az aritmetika az összeadás, kivonás, szorzás és osztás alapjaira terjed ki.
- Gyakoroljon kérdéseket. Az aritmetikai feladatok újra és újra elvégzése a legjobb módszer az alapok helyes memorizálására. Keressen olyan szoftvereket, amelyek sokféle matematikai problémát kínálnak Önnek. Ezenkívül keressen problémákat az időkeretekkel a sebesség javítása érdekében.
- Az aritmetikai problémákat online is megtalálhatja, és számtani alkalmazásokat tölthet le mobileszközére.

2. lépés: Folytassa az előalgebrával
Ez a gyakorlat biztosítja azokat az alapvető elemeket, amelyekre szüksége lesz az algebra -problémák későbbi megoldásához.
- Ismerje meg a törteket és a tizedesjegyeket. Megtanulja törtek és tizedesek hozzáadását, kivonását, szorzását és osztását. Ami a törteket illeti, megtanulja a törtek kivonását és a kombinált számok fordítását. Ami a tizedesjegyeket illeti, megérti a helyértékeket, és képes lesz használni a tizedeseket a történetproblémákban.
- Ismerje meg az arányokat, az arányokat és a százalékokat. Ezek a fogalmak segítenek megtanulni összehasonlítani.
- Mutassa be az alapvető geometriát. Meg fogja tanulni a 3D formákat és fogalmakat. Megtanulhat olyan fogalmakat is, mint a terület, a kerület, a térfogat és a felület, valamint a párhuzamos és merőleges vonalakról és szögekről szóló információkat.
- Ismerjen meg néhány alapvető statisztikát. A pre-algebrában a statisztika bevezetője általában olyan vizuális elemeket tartalmaz, mint például grafikonok, szórási diagramok, bélyegző diagramok és hisztogramok.
- Ismerje meg az algebra alapjait. Ez magában foglal olyan fogalmakat, mint a változókat tartalmazó egyszerű egyenletek megoldása, az olyan tulajdonságok megismerése, mint az elosztási tulajdonság, egyszerű egyenletek rajzolása és az egyenlőtlenségek megoldása.
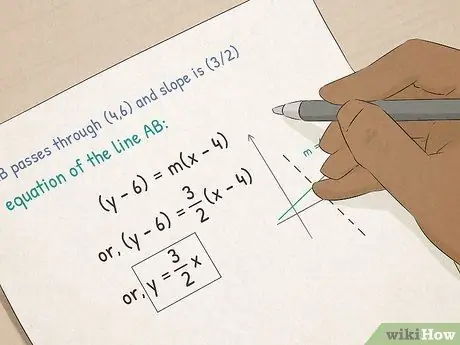
3. lépés. Előrelépés az Algebra I
Az algebra első évében megismerheti az algebra alapvető szimbólumait. Azt is megtanulja, hogy:
- Változókat tartalmazó egyenletek és egyenlőtlenségek megoldása. Megtanulja, hogyan lehet ezeket a problémákat papíron megoldani és képekkel megoldani.
- Mesebeli problémák megoldása. Meg fogsz lepődni, hogy mennyi mindennapi problémával fogsz szembenézni a jövőben, amelyek megkövetelik az algebrai történetfeladatok megoldásának képességét. Például az algebra segítségével megtudhatja a bankszámláján vagy befektetésén keresett kamatlábat. Az algebra segítségével kitalálhatja, mennyi ideig kell utaznia az autó sebessége alapján.
- Dolgozzon a kitevőkkel. Amikor elkezdi megoldani a polinomiális egyenleteket (számokat és változókat tartalmazó kifejezéseket), megérti, hogyan kell használni a kitevőket. Ez valószínűleg tudományos jelöléssel ellátott gyakorlatokat is tartalmaz. Miután elsajátította a kitevőket, megtanulhat polinomiális kifejezéseket összeadni, kivonni, szorozni és osztani.
- Négyzet és négyzetgyök feladatok megoldása. A téma elsajátítása során képes lesz megjegyezni a sok szám négyzetét. Ezenkívül négyzetgyökű egyenletekkel is dolgozhat.
- Ismerje meg a függvényeket és a grafikonokat. Az algebrában a grafikus egyenletekről fog tanulni. Megtanulja, hogyan kell kiszámítani egy egyenes meredekségét, hogyan kell egyenletet elhelyezni pont-lejtés alakban, és hogyan kell kiszámítani az egyenes x-és-y-szeletét a lejtés-metszés űrlap segítségével.
- Ismerje meg az egyenletrendszert. Néha két különböző egyenletet kap az x és y változókkal, és mindkét egyenlethez x vagy y helyett kell megoldania. Szerencsére sok trükköt megtanulhat ezeknek az egyenleteknek a megoldására, beleértve a grafikázást, a helyettesítést és az összeadást.

4. lépés. Tanulmányozza a geometriát
A geometriában megismerheti a vonalak, szegmensek, szögek és alakzatok tulajdonságait.
- Számos tételt és következtetést memorizál, amelyek segítenek megérteni a geometria szabályait.
- Megtanulja, hogyan kell kiszámítani egy kör területét, hogyan kell használni a Pitagorasz -tételt, és hogyan lehet megtalálni a kapcsolatot egy speciális háromszög szögei és oldalai között.
- Sok geometriai kérdést fog látni a jövőbeni szabványosított tesztekben, mint például a SAT, az ACT és a GRE.
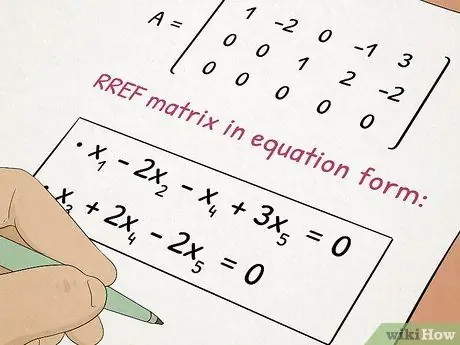
5. lépés Vegye ki az Algebra II osztályt
Az Algebra II az Algebra I -ben tanult fogalmakra épít, és olyan bonyolult témákhoz ad hozzá, mint a másodfokú egyenletek és mátrixok.
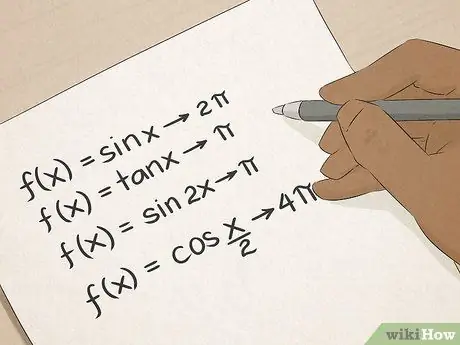
6. lépés. Mester trigonometria
Ismeri a trigonometriai kifejezéseket: szinusz, koszinusz, érintő stb. A trigonometria sok gyakorlati módszert megtanít a szögek és vonalhosszak kiszámítására, és ezek a készségek felbecsülhetetlen értékűek az építőiparban, építészetben, mérnöki munkában vagy földmérésben dolgozók számára.
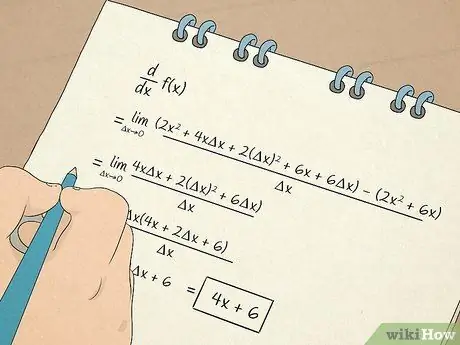
7. lépés Végezze el a számításokat
A számítás megfélemlítőnek tűnhet, de csodálatos eszköz a számok viselkedésének vagy a körülötted lévő világ megértéséhez.
- A Calculus megtanítja a funkciókat és korlátokat. Látni fogja a hasznos függvények számbeli viselkedését, beleértve az e^x és a logaritmikus függvényeket.
- Azt is megtanulja, hogyan kell kiszámítani és dolgozni a származékos termékekkel. Az első derivált információt ad az egyenlet érintő egyenesének meredeksége alapján. Például egy derivált megmondja, hogy milyen sebességgel változik valami nemlineáris helyzetben. A második derivált megmondja, hogy a függvény növekszik -e vagy csökken egy bizonyos intervallumon keresztül, így meghatározhatja a függvény homorultságát.
- Az integrálok megtanítják, hogyan kell kiszámítani a görbe alatti területet és annak térfogatát.
- A középiskolában a számítások általában sorozatokban és sorozatokban végződnek. Bár a diákok nem sok alkalmazást látnak az áramkörök számára, az áramkörök fontosak azok számára, akik differenciálegyenleteket tanulnak.
3. rész a 6-ból: Matematika alapjai-Mester kiegészítés

1. lépés. Kezdje a "+1" tényekkel
Ha 1 -et ad hozzá egy számhoz, akkor a számsor legmagasabb számához jut. Például 2 + 1 = 3.
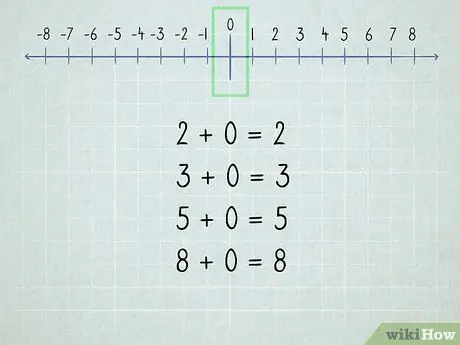
2. lépés. Értse meg a nullát
Minden nullához hozzáadott szám ugyanaz, mert a "nulla" azt jelenti, hogy "nincs".

Lépés 3. Ismerje meg a kettős számokat
A több szám olyan probléma, amely két egyenlő szám hozzáadását jelenti. Például a 3 + 3 = 6 példa több számot tartalmazó egyenletre.

Lépés 4. Használja a leképezést a további hozzáadási megoldások megismeréséhez
Az alábbi példában azt tanulhatja meg, hogy feltérképezi, mi történik, ha hozzáadja a 3 -at az 5 -hez, a 2 -hez és az 1 -hez. Próbálja ki az "add by 2" problémát.

5. lépés. Folytassa, amíg a szám meg nem haladja a 10 -et
Tanuljon meg három számot összeadni, hogy 10 -nél nagyobb számot kapjon.
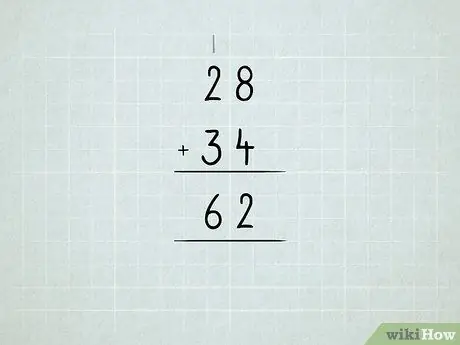
6. Összeadja a nagyobb számokat
Ismerje meg az egységek átcsoportosítását tízesekre, tízeseket százokra stb.
- Először add össze a jobb oldali oszlopban található számokat. 8 + 4 = 12, ami azt jelenti, hogy van 1 10 -es és 2 -es szám. Írja be a 2 -es számot az egységek oszlopba.
-
Írja az 1 -es számot a tízes oszlopba.
-
Adja hozzá a tízes oszlopot teljes egészében.
4. rész a 6-ból: Matematikai alapok-redukciós stratégiák

1. lépés: Kezdje a "visszafelé 1 számjeggyel"
Ha 1 -et kivonunk egy számból, akkor 1 számot viszünk vissza. Például 4 - 1 = 3.

2. lépés. Tanuljon meg kettős számokat kivonni
Például, ha hozzáadja az 5 + 5 számokat, hogy 10 -et kapjon. Csak írja vissza az egyenletet, hogy 10 - 5 = 5 legyen.
- Ha 5 + 5 = 10, akkor 10 - 5 = 5.
-
Ha 2 + 2 = 4, akkor 4 - 2 = 2.

3. lépés. Jegyezze meg a család tényét
Mint például:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

4. lépés. Keresse meg a hiányzó számokat
Például _ + 1 = 6 (a válasz 5).

5. lépés. Jegyezze meg a kivonás tényét 20 -ra

6. lépés Gyakorold, hogy kölcsönzés nélkül vonjunk le egyjegyű számokat a kétjegyű számokból
Vonja ki az egyes oszlopban lévő számokat, és csökkentse a tízes oszlop számát.
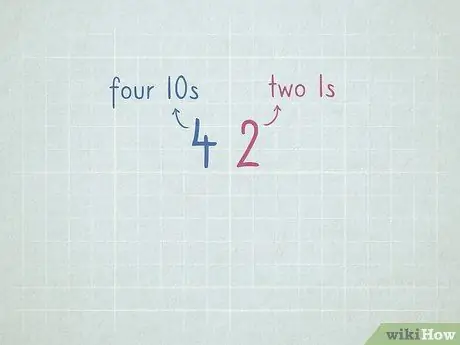
7. lépés: Gyakorolja a helyértéket, hogy felkészüljön a kölcsönzéssel történő kivonásra
- 32 = 3 szám 10 és 2 szám 1.
- 64 = 6 szám 10 és 4 szám 1.
- 96 = _ 10. szám és _ 1. szám.
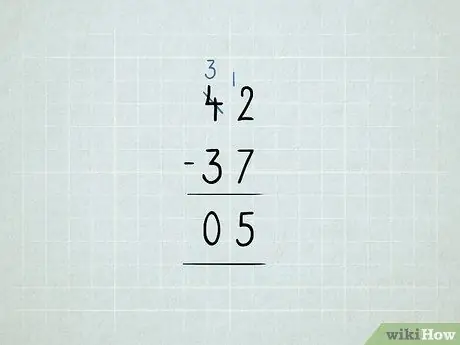
8. Lépés
- 42 - 37 -et szeretne levonni. Először az egység oszlopban 2-7 -et kell kivonni. Kiderült, nem sikerült!
-
Kölcsönözze a 10 -es számot a tízes oszlopból, és helyezze az egyek oszlopba. Most 3 10 van a 4 10 helyett. Most 12 1 van a 2 1 helyett.
-
Először vonja le az egységek oszlopát: 12 - 7 = 5. Ezután ellenőrizze a tízes oszlopot. Mivel 3 - 3 = 0, nem kell leírnia a 0 számot. A válasz 5.
5. rész a 6-ból: Matematika alapjai-Mester szorzás

1. lépés Kezdje az 1 -es számmal és a 0 -val
Minden 1 -gyel megszorozott szám ugyanaz, mint maga a szám. Bármely szám szorozva 0 -val, nulla.

2. lépés. Jegyezze meg a szorzótáblát

3. lépés. Gyakoroljon egy számjegyű szorzási feladatokat

Lépés 4. Szorozza meg a 2 jegyű számot az 1 jegyű számmal
- Szorozzuk meg a jobb alsó számot a jobb felső számmal.
-
Szorozzuk meg a jobb alsó számot a bal felső számmal.
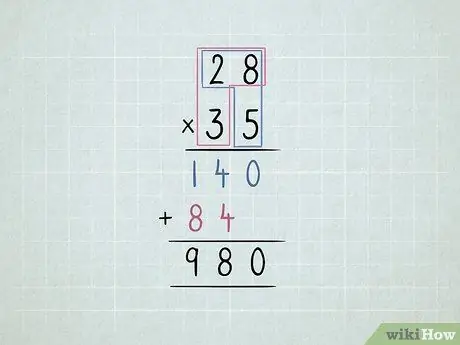
5. lépés Szorozzon meg 2 kétjegyű számot
- Szorozzuk meg a jobb alsó számot a jobb felső számmal, majd a bal felső számmal.
-
Mozgassa a második sort egy számjeggyel balra.
- Szorozzuk meg a bal alsó számot a jobb felső számmal, majd a bal felső számmal.
-
Adja hozzá az összes oszlopot.
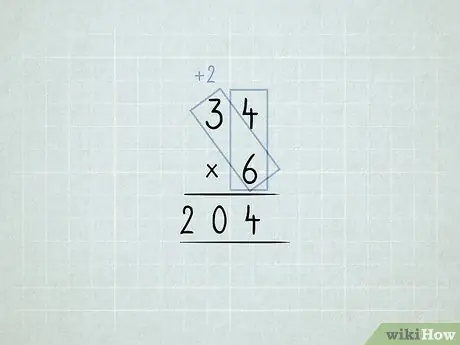
6. lépés: Szorozza meg és csoportosítsa újra az oszlopokat
- 34 x 6 -ot szeretne megszorozni. Kezdje az egység oszlop szorzásával (4 x 6), de nem lehet 24 1 -es az egyek oszlopban.
-
Tároljon 4 1 -et az egységek oszlopban. Lépjen 2 10 -et a tízes oszlopba.
-
Szorozzuk meg a 6 x 3 -at, ami 18 -at ad.
6. rész a 6-ból: Matematikai alapismeretek-A felosztási feladatok feltárása

1. Lépés: Gondoljon az osztásra, nem pedig a szorzásra
#* Ha 4 x 4 = 16, akkor 16 /4 = 4.
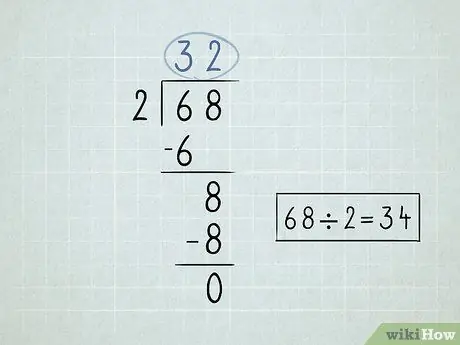
2. lépés. Írja le a megosztási problémáját
- Ossza meg az osztószimbólumtól balra lévő számot vagy osztót az osztó szimbólum alatti első számmal. Mivel a 6 /2 = 3, a 3 -as számot az osztási szimbólum fölé írná.
-
Szorozzuk meg az osztási szimbólum feletti számot az osztóval. Vigye az eredményt az osztás szimbólum alatti első szám aljára. Mivel 3 x 2 = 6, akkor a 6 -os számot leengedi.
- Vedd ki a 2 számot, amit leírtál. 6 - 6 = 0. A 0 -t üresen hagyhatja, mert általában nem 0 -val kezdi a számokat.
-
Húzza le a második számot, amely az osztási szimbólum alatt található.
- Oszd el a számot, amelyet lehoztál az osztóval. Ebben az esetben 8 /2 = 4. Írja a 4 -es számot az osztási szimbólum fölé.
-
Szorozzuk meg a jobb felső számot az osztóval, és vigyük lefelé. 4 x 2 = 8.
-
Vonja ki ezeket a számokat. Az utolsó kivonás nullát ad vissza, ami azt jelenti, hogy megoldotta a problémát. 68 x 2 = 34.

Lépés 3. Számítsa ki a maradékot is
Az osztók egy része nincs teljesen felosztva más számokra. Ha befejezte az utolsó kivonást, és nincs több levezethető szám, akkor az utolsó szám a maradék.






